Als je de lijst van Corona-besmettingen per land overloopt valt het je niet meteen op, maar de meeste getallen beginnen met 1, 2 of 3. En dat is toch bizar, want we hebben toch 9 mogelijkheden voor het eerste cijfer, met bijhorende kans van 1 op 9 (11%) Klopt niet. En er is meer: bijna alles om ons heen volgt deze wetmatigheid: de kans dat een getal begint met ‘1’ is 30%, de kans op een 9 slechts een kleine 5%. Neem maar de proef op de som en turf de getallen in je krant: je zal zien dat meer dan de helft van de getallen start met 1, 2 of 3. Ik vind dit waanzinnig! Het is de fysische wereld die spartelt in het keurslijf van ons positiestelsel.

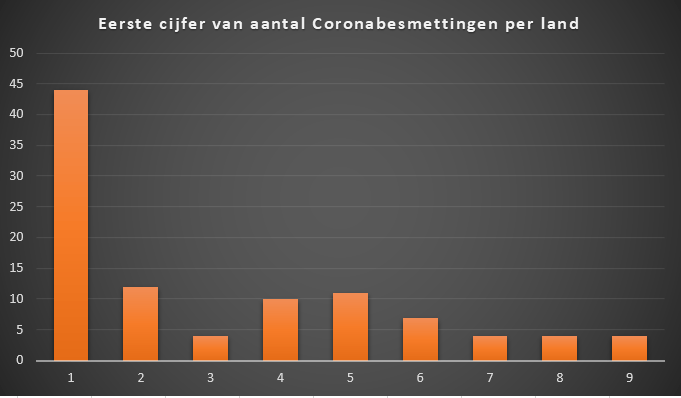
Ik poneerde dit gisteren bij een vriend en we namen samen de proef op de som: we namen de krant en ik turfde het aantal keer dat een getal met een bepaald cijfer begon. En na enkele pagina’s van De Tijd doorploegd te hebben op zoek naar getallen was het overduidelijk: hoe hoger het cijfer hoe minder kans dat het een startcijfer is. Hieronder de uitslag waaruit overduidelijk blijkt dat de kans op het eerste cijfer niet gelijk verdeeld is.

We hebben daarna zowel het aantal inwoners als de oppervlakte van elk land op de zelfde manier geanalyseerd en we komen tot de zelfde verrassende vaststelling dat het cijfer 1 het meest voorkomt of het nu gaat over een aantal inwoners of een oppervlakte. Het maakt zelfs niet uit in welke eenheid de oppervlakte wordt beschouwd vierkante km, vierkante mijl, hectares,… de uitkomst zal eenzelfde beeld geven.

Ook ik vond dat op het eerste zicht verrassend en zelfs verbluffend: hoe is het mogelijk? Het fenomeen blijkt beschreven te zijn door de wet van Benford, en dat is wat wikipedia ons vertelt:

“De wet van Benford beschrijft de frequentieverdeling van het begincijfer van getallen in grote dataverzamelingen waarin een beperkte mate van stochasticiteit optreedt. De wet van Benford werd in 1881 ontdekt door de Amerikaanse wiskundige en astronoom Simon Newcomb, maar kreeg grote bekendheid door de herontdekking en publicaties in 1938 van Frank Benford, een fysicus die zijn hele leven bij het Amerikaanse bedrijf General Electric heeft gewerkt.”

De wet van Benford drukt op volgende wijze uit wat de kans is op een startcijfer ‘d’:

Toegepast op het cijfer ‘1’ geeft dit:

d	1	2	3	4	5	6	7	8	9
kans (%)	30,1	17,6	12,5	9,7	7,9	6,7	5,8	5,1	4,6

Hoe kunnen we dit verklaren? Er lijkt niet echt een eenvoudige wiskundige verklaring te zijn. Wat we wel kunnen aantonen is dat als we een frequentieverdeling beschouwen van de startcijfers die onafhankelijk moet zijn van de gebruikte eenheid, we op een logaritmische frequentieverdeling komen, zoals hierboven beschreven.  Concreet wil dat zeggen dat we er van uitgaan dat de eenheid voor bepaalde grootheden geen invloed heeft op het resultaat. Want het is de mens die heeft uitgevonden hoelang een meter is. Daar kan de natuur of de werkelijkheid der dingen zich niets van aantrekken.

Eens je beseft dat het switchen van de ene eenheid naar een andere in feite een vermenigvuldiging is, kan je het fenomeen begrijpen door er een cirkelvormige rekenlat bij te halen. Jammer genoeg heb ik er geen in bezit, maar op een Breitling Navitimer zijn de buitenste rijen getallen die je kan verdraaien ten opzichte van elkaar eigenlijk een rekenlat. Wat kan je daarmee doen? Getallen vermenigvuldigen door te draaien, zie ook: De geheimen van grootvaders rekenlat. Graag breng ik je aandacht op het feit dat meer dan de helft van de cirkel getallen zijn die beginnen met een 1, 2 of 3. Dus hoe meer we willekeurige getallen gaan vermenigvuldigen hoe meer we zullen voldoen aan de wet van Benford. En we moeten hierbij ook opmerken dat we meeste natuurwetten gebaseerd zijn op een vermenigvuldiging, denk maar aan F=ma, de gravitatiewet, wetten van Maxwel,…

Een test die je eenvoudig zelf kunt doen is willekeurig gekozen getallen A, B en C vermenigvuldigen op een rekenmachine en turven wat de frequentieverdeling is van uitkomst AxBxC, en na een tijdje zal de wet van Benford zich aan je openbaren: cijfer 1 zal beduidend meer voorkomen dan de andere cijfers.

Geldt de wet voor alle reeksen van getallen? Nee, dat ook weer niet. Om dergelijke verdeling te hebben moeten de gegevens over meerdere grootte-ordes gespreid zijn. Dus de lengtes van personen vallen hier bijvoorbeeld niet onder. Ook een lijst van hoogste bergtoppen niet, maar een lijst van alle bergen op aarde dan weer wel.

Het is contra-intuïtief omdat het het begrip ‘ad random’ een beetje op z’n kop zet. Als je getallen door een computer ad random laat bepalen dan zullen ze niet aan de wet van Benford voldoen. Het zijn dan ook geen werkelijke dingen die gemeten of geteld kunnen worden, maar enkel een getal genomen uit een verzameling van getallen, zoals een lotto-trekking. Als je op een bepaald moment een aantal gegevens moet verzinnen, b.v. facturen of in een wetenschappelijk onderzoek, kan je maar beter zorgen dat deze voldoen aan de wet van Benford. Want je zou niet de eerste fraudeur zijn die tegen de lamp loopt doordat z’n data zo verzonnen is dat alle startcijfers gelijk verdeeld voorkomen.

Tot slot terug naar het Corona-virus. Een prachtig voorbeeld van exponentiële groei in de huidige fase. Zie ook: Dromen over het getal e. Wanneer je een bedrag laat opbrengen op de bank zal het totaal bedrag groeien. Maar om van 100 euro naar 200 euro te groeien moet het bedrag verdubbelen (groei: 50%), maar daarentegen om te groeien van 800 euro naar 900 euro hoeft het bedrag maar te groeien met 12,5%. Daarom blijft het totaalbedrag langer ‘hangen’ tussen 100 en 200 euro en groeit het sneller door van 800 naar 900 euro. Wat we terugvinden in de frequentieverdeling van alle bedragen die op de bank staan, daarvan zal 30% ook starten met een ‘1’ ! Ook voor het aantal Corona-besmettingen is het een verdubbeling om van 1000 naar 2000 besmettingen te gaan, maar slecht een kleine groei om van 8000 naar 9000 besmettingen te gaan. En dat raakt volgens mij de ziel van deze mooie wetmatigheid.

Getallen die de Benford-wet volgen zijn echt en staan met beide voeten in de werkelijkheid.

Het is op dit moment (begin maart 2020) nog koffiedik kijken hoeveel het maximale aantal besmettingen per land zal zijn, maar één ding weten wel wel: het zal voldoen aan de wet van Benford.

En in tijden van onzekerheid, is dit misschien een lichtpuntje.

Benford-verdeelde groeten aan iedereen,

T.E.