Geplaatst op door Tijs Essel · 1 reactie

Over structuren en de wet van Hooke

‘Ut tensio sic vis’, zo klinkt de wet van Hooke in het Latijn. Zoals de verlenging is, zo is de kracht. Het drukt uit dat er een evenredigheid is tussen de kracht op een voorwerp en de verlenging. Denk maar aan een veer van een weeghaak. Bij het verdubbelen van de last zal ook de verlenging verdubbelen. De wet van Hooke stipuleert dat alle materialen zich op deze manier gedragen. Een mooie wet, alleen… geen enkel materiaal volgt deze wet!

kx-law-Hooke-F-force-length-displacement

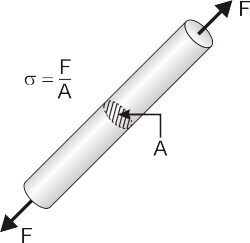
De wet van Hooke kan men ternauwernood een wet noemen, toch zeker in vergelijking met de quasi algemeen geldende natuurwetten van Newton, z’n eeuwige rivaal. De relatie wordt tegenwoordig echter steeds uitgedrukt als een evenredigheid tussen de spanning (zie Over structuren en het spannend verhaal van trekken en duwen) en rek, wat niet de verlenging is maar de relatieve verlenging. Deze begrippen waren nog niet zo vertrouwd in de tijd van Hooke. De wet van Hooke ziet er dan dus als volgt uit:

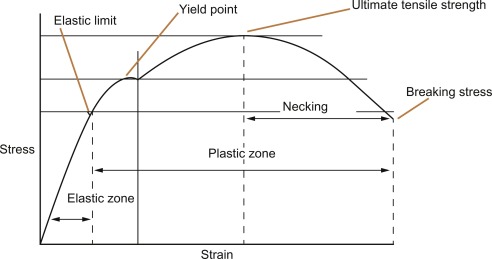
Maar zoals reeds aangekondigd zijn er geen materialen die zich perfect houden aan deze wet. Alleen al om de simpele reden dat geen enkel materiaal oneindig sterk is. Ieder materiaal heeft z’n specifieke spanning-rek curve maar één ding is zeker: op een zeker moment is er een breuk. Op onderstaande grafiek is het duidelijk dat er bij kleine rekken een lineair gedrag is, dat is het elastisch gebied, maar verder hebben verschillende materialen uiteenlopend gedrag bij oplopende rek, zoals je op onderstaande grafiek kan zien.

Typical-stress-strain-curves-of-polymers-tested-at-different-temperatures-curves-a-c

De rek. Daar moeten we het eerst eens over hebben. Thomas Young deed ooit een vergeefse poging om dit aan de mensheid uit te leggen, jammer genoeg was er geen enkele sterveling op aarde die een jota begreep van wat hij juist bedoelde… “We may express the elasticity of any substance by the weight of a certain column of the same substance, which may be denominated the modulus of its elasticity, and of which the weight is such, that any addition to it would increase it in the same proportion as the weight added would shorten, by its pressure, a portion of the substance of equal diameter.” Toch wordt de elasticiteitsmodulus naar hem genoemd: de Young-modulus.

Hier volgt mijn poging om het bevattelijk uit te leggen: Rek is de mate van relatieve verlenging of verkorting van een materiaal. Wiskundig gezien is een verkorting een negatieve rek, soms wordt ook wel een het begrip stuik gebruikt om een verkorting aan te duiden. De algemene definitie van rek is de verhouding van de verlenging tot de oorspronkelijke lengte:

Hieruit volgt dat de rek een dimensieloze eenheid is. Een rek van 1 betekent dat de oorspronkelijke lengte verdubbeld is. Meestal is de relatieve verlenging echter subtieler van aard en wordt de rek uitgedrukt in promille of micron. Soms wordt ook de eenheid ‘S’ (strain) gebruikt om de hoeveelheid rek aan te geven.

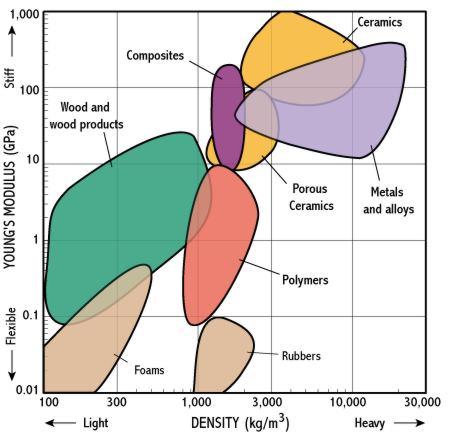
De verhouding tussen de spanning en de rek wordt de elasticiteitsmodulus E van een materiaal genoemd, het geeft de weerstand tegen rek aangeeft. Stijve materialen hebben een hoge elasticiteitsmodulus en flexibele materialen een lage. Je kan je zo wel inbeelden dat rubber een zeer lage elasticiteitsmodulus heeft en glas heeft dan weer een hoge elasticiteitsmodulus. Hieronder zie je de de elasticiteitsmodulus (of Young-modulus) uitgezet voor bepaalde materiaalgroepen. In onderstaande grafiek wordt de elasticiteitsmodulus (Young’s Modulus) uitgezet ten opzichte van het soortelijk gewicht van de materialen, zo zie dat grosso modo zwaardere materialen eerder stijver zijn.

Young Modulus

We moeten dus vaststellen dat de wet van Hooke in feite meer een soort van vereenvoudiging is van het gedrag van materialen bij kleine rekken, maar dat de spanning-rek curve tot breuk per materiaal sterk kan verschillen. Glas zal zoals wel bekend plots breken, staal kan behoorlijk vervormen vooraleer er breuk is. Het gedrag van een materiaal na het elastisch gebied wordt het plastisch gebied genoemd. Het punt waarop een materiaal het elastisch gebied verlaat wordt het vloeipunt genoemd. Dat glas plots breekt heeft te maken met het ontbreken van een plastisch deel van de curve, een eigenschap van brosse materialen.

stress strain

En mocht je nu denken dat we vooral sterke en stijve materialen nodig hebben om veilige gebouwen te maken… dan heb je het helemaal mis! En dat heeft dan weer alles te maken met vervormingsenergie. Waarover later uiteraard meer…

Tot breuk uitgerekte groeten,

T.E.

In deze reeks:

Over structuren en de derde wet van Newton

Over structuren en het spannend verhaal van trekken en duwen

P.S.

Er wordt in de wandelgangen gefluisterd dat het, mede door het toedoen van de niet aflatende ijver van Newton om de herinnering aan Hooke zoveel mogelijk uit te wissen, geen portretten zijn overgebleven van de arme man. Het portret hieronder is een hedendaagse poging op basis van de overgeleverde geschreven info.

 

13_Portrait_of_Robert_Hooke

Geplaatst op door Tijs Essel · 1 reactie

Over structuren en het spannend verhaal van trekken en duwen

Er wordt niet enkel in wetenschappelijke kringen over spanning gesproken. Spanningen kunnen hoog oplopen tussen mensen of landen. Een boek kan spannend zijn. Ons dagelijks leven zit uiteraard ook vol stress (of spanning). We geven aan dat het een toestand is die in extremis kan leiden tot ruzie, oorlog, ontknoping of een zenuwinzinking… Een zwaar belastende job geeft je veel stress. De analogie voor materialen is zeer gelijklopend: een zwaar belast materiaal zal onder hoge spanning staan, totdat de spanning te hoog oploopt en het materiaal bezwijkt.

main-qimg-11a13227b43cff2cde6b30cc92816448

Als voorproefje voor dit schrijven had ik verkondigd dat krachten niet bestaan in realiteit (Over structuren en de derde wet van Newton), dat zal ik hier zeker niet ontkrachten, wel toelichten. Krachten bestaan niet in de zin dat een krachtvector een wiskundige constructie is zoals een rechte of een lijnstuk en daardoor geen breedte heeft en daarmee moeilijk verzoenbaar is met de werkelijkheid die zich in alle ruimtelijkheid voor ons ontplooit. In deze werkelijkheid is de spanning die optreedt in materialen een veel betere maatstaf van de toestand van een materiaal dan kracht. Bouwkundigen zullen daarom aan het einde van het verhaal vooral geïnteresseerd zijn in de spanningen die heersen in de materialen waarin constructies zijn opgebouwd, deze spanningen worden gedefinieerd als de kracht per oppervlakte:

stress_pic2

De Griekse kleine letter sigma wordt in de sterkteleer meestal als symbool gebruikt voor spanning en deze wordt uitgedrukt in Newton per vierkante meter (N/m²), algemene spanningen in de natuurkunde worden veelal uitgedrukt met het symbool p (pressure). De eenheid van spanning is pascal (Pa) waarbij 1 Pa = 1 N/ m². Deze eenheden maken deel uit van de uniforme internationale standaardeenheden (het SI-stelsel), en het pleit zeer voor de wereldwijde samenwerking van wetenschappers dat bijna alle landen diezelfde eenheden gebruiken. Het zou werkelijk onhandig zijn als bepaalde landen spanning in pakweg pond per vierkante duim zouden uitdrukken. Het is dan in het licht van de uniformisering betreurenswaardig dat we nota bene de Verenigde Staten van Amerika terug vinden in het rijtje van landen, naast Myanmar en Liberia, die niet officieel het SI-stelsel hebben ingevoerd. Dat maakt overigens dat bouwkundige naslagwerken (en ik vermoed bij uitbreiding veel wetenschappelijke boeken) uit de VS quasi waardeloos zijn in de rest van de wereld en de ontgoocheling is dan ook groot wanneer een aangekocht boek in deze middeleeuwse eenheden blijkt opgesteld te zijn. Voor degenen die toch de omrekening willen doen: 1 psi = ca. 6895 Pa, waarbij psi staat voor ‘pounds per square inch’.

psi kPa

Maar laten wij ons niet al te zeer verkneukelen in deze trans-Atlantische bizariteit. Wanneer wij spreken over een bloeddruk die 14 over 7 is dan spreken wij ook helemaal niet in pascal of N/m², maar hebben we het over kwikdruk in cmHg. Het was gebruikelijk om de luchtdruk te meten met behulp van een kolom kwik, de normale atmosferische luchtdruk bedraagt zo’n 760 mmHg. Kwik is veel zwaarder dan andere vloeistoffen, en daarom handiger qua formaat, zo is het historisch gegroeid dat mmHg de eenheid voor bloeddruk is geworden en 1 mmHg is trouwens gelijk aan ca. 133,322 Pa. De schaal is nu zo ingeburgerd dat het standaard is om lichaamsvloeistoffen uit te drukken in mmHg, voor alle andere toepassingen is het SI-stelsel de standaard. Een normale bloeddruk van 120 mmHg komt overeen met een druk van 16 kPa.

Het feit dat de luchtdruk op aarde schommelt rond 100 kPa (komt overeen met 1 bar) is op het eerste zicht verwonderlijk. Op ieder van ons heerst er een druk die equivalent is met een waterkolom van 10 m. Dat is een behoorlijke druk en zoals veel zaken die niet opvallen, valt hij pas op wanneer we hem moeten missen. Zoals op de maan, waar zonder ruimtepak onze lichaamssappen zouden koken, bij het ontbreken van voldoende luchtdruk, wat steeds tot een gewisse dood zou leiden. Dat doet me denken aan de koningin van de nacht uit De Toverfluit die zingt: “Der Hölle Rache kocht in Meinem Herzen”. Het bloed kookt in haar hart! Extreme drukken vinden we in het heelal: zowel het bijna absolute vacuüm in de verste leegtes van ons universum als de werkelijk extreme drukken binnen in een neutronenster. Daar heersen zo’n extreme drukken dat het onbegonnen is om ook maar enige vergelijking te maken. Toch een poging: een theelepeltje neutronenster weegt 10 miljoen ton, of evenveel als 50 keer het gewicht van de grootste containerschepen die er bestaan…

neutronenster

Maar terug naar spanningen in materialen, deze zijn nog een paar grootte ordes groter dan de luchtdruk en worden meestal uitgedrukt in MPa (één miljoen Pa). De maximale trekspanning in een materiaal wordt de treksterkte genoemd. Zo is de treksterkte van normaal staal 420 MPa. Hout is tien keer minder sterk: de sterkte van dennenhout is 40 MPa. Een enorm sterk materiaal is een koolstof nanobuis met een sterkte van maar liefst 62.000 MPa. En de treksterkte van beton sluit vele lijstjes van materialen af met een bedroevende 2 MPa.

Hoe is het mogelijk dat we zoveel gebouwen hebben opgetrokken met zo’n zwak materiaal als beton? Om dit te verklaren moeten we begrijpen dat spanningen zich manifesteren in twee verschijningsvormen: drukspanningen en trekspanningen. De luchtdruk is ontegensprekelijk een drukspanning, maar de treksterkte van materialen gaat over de trekspanningen. Beton heeft weliswaar een lage treksterkte, maar kan zeker z’n mannetje staan als het over druksterkte gaat. Dat is trouwens z’n sterkste punt, sterkteklassen van beton verwijzen altijd naar de druksterkte. Zo is C30/37 een beton met een karakteristieke druksterkte van 30 MPa op een proefcilinder (de 37 MPa slaat op de druksterkte op een proefkubus). Gewapend beton is een mooi huwelijk tussen beton en staal waarbij beton de drukspanningen voor z’n rekening neemt het staal de trekspanningen. Het gezegende aan dit huwelijk is dat beide materialen op dezelfde manier reageren op temperatuurschommelingen en dat beton het staal beschermd tegen corrosie.

Reinforced-Concrete

Dat spanningen een ander fenomeen zijn dan krachten kan je zelf ervaren als je een scherp potlood tussen duim en wijsvinger houdt en die samendrukt. De kracht in het potlood is uiteraard dezelfde, maar bij de kleine oppervlakte van de punt zal de spanning groter zijn (kracht gedeeld door kleiner oppervlak) en dat zie je ook afgetekend in je huid. Het is een welbekend voorbeeld dat een olifant gemakkelijker door het zand stapt dan iemand op stiletto’s. Dat heeft niets te maken met de kracht, maar alles met de spanning, want de spanning op de grond van de stiletto’s is veel groter dan de spanning veroorzaakt door een olifantenpoot. Laat ons dat eens snel berekenen voor een dame van 60 kg met hakken van diameter 1 cm diameter en een olifant van 5 ton met 4 poten met een diameter van 30 cm.

stiletto-elaphant

De druk onder een stiletto is wel 20 keer hoger dan de druk onder een olifantenpoot, daarmee loopt de olifant beduidend vlotter door het zand dan de dame in kwestie en begrijpt iedereen beduidend beter het verschil tussen krachten en spanningen.

Van de olifantenpoot naar een stevige kolom in een gebouw is maar een kleine stap het zijn allebei elementen waar er drukspanningen in heersen. Een mooi voorbeeld van trekspanningen zijn de spanningen in een kabel, en bij uitbreiding alle constructies die gebruik maken van kabels. Hangbruggen en tuibruggen zijn pareltjes van voorbeelden.

Cable-stayed-bridge-1000x500

Spanning. Het doet wat met een mens. Maar wat doet spanning met materialen? Vroeg of laat komt het tot breuk en sterke materialen zijn bestand tegen grote spanningen, maar hoe reageert een materiaal op spanning? We hadden het vorige keer over Newton en z’n wet over actie en reactie die aan de basis licht van de krachtenanalyse van een structuur. Maar minstens even belangrijk voor de bouwkundige analyse van structuren is de wet van z’n tijdsgenoot en rivaal: Robert Hooke. De wet van Hooke is werkelijk de Alfa en de Omega van de sterkteleer.

In een volgend schrijven zal de wet van Hooke onder de loep genomen worden, waarmee dit schrijven eindigt in spanning!

Spannende groeten,

T.E.

kisspng-hooke-s-law-shear-stress-strength-of-materia

Geplaatst op door Tijs Essel · 2 reacties

Over structuren en de derde wet van Newton

Newtons bewegingswetten toepassen op bouwkundige structuren lijkt op het eerste zicht een nutteloze onderneming. Structuren worden immers niet verondersteld te bewegen. Het liefst hebben we ze statig, solide en immobiel (vandaar ook immobiliën). Teveel beweging, laat staan een instorting, is uit den boze. Toch zijn structuren doordrongen van de derde wet van Newton. Die van actie en reactie! 

Structuren zijn er overal. Zoals iemand met een hamer overal nagels ziet en een leraar Nederlands overal taalfouten ziet, zo ziet een bouwkundige overal structuren. En dan zeker niet alleen in gebouwen. Ook een stoel, een kast, een ei, een boom, een huisjesslak, een verkeerslicht, een kartonnen doos, een glas en zelfs ons eigen lichaam zijn allemaal stuk voor stuk structuren. Het is niet voor niets dat ze soms spreken van een ‘kathedraal’ van een lichaam! En van simpel karton worden bouwkundigen werkelijk poëtisch: wat een prachtige mini-vakwerkjes komen immers te voorschijn wanneer je karton doormidden snijdt!

profipack_golfkarton_platen-7

De derde wet van Newton stelt dat wanneer een voorwerp A een kracht op een ander voorwerp B uitoefent, deze gepaard gaat met een even grote maar tegengesteld gerichte kracht van B op A. De woorden actie en reactie zijn wat misleidend want de krachten komen gelijktijdig voor, de ene is niet de oorzaak van de andere. De nagel slaat net zozeer op de hamer als de hamer op de nagel, met een even grote en tegengestelde kracht. Als een bokser z’n collega een welgemikte uppercut geeft, dan is het een magere troost voor laatstgenoemde dat de kracht van z’n kin terug op de bokshandschoen van z’n opponent precies even groot is. ‘Eat this!’, kan hij denken, net voor hij KO gaat, terwijl hij languit op de grond neergezijgd opnieuw een treffend voorbeeld is van de derde wet van Newton als interactie tussen z’n lichaam en de grond. Reciprociteit van krachten (of wederkerigheid) is een begrip die wellicht meer de lading dekt van de derde wet van Newton.

boksers met krachten

Ik weet niet welke job jij uitoefent, welke strijd er bij jou moet gestreden worden, maar bouwkundigen vechten tegen de zwaartekracht. Ze vechten tegen nog wel meer zaken, maar in hoofdzaak tegen de zwaartekracht, die vijand nummer één is van bouwkundige constructies. Het instorten van bruggen of gebouwen is een gebeurtenis waarbij de zwaartekracht wint. Het gebeurt gelukkig niet veel tijdens de levensduur waarvoor een constructie ontworpen is, maar als je maar lang genoeg wacht (op een geologische schaal), wint de zwaartekracht altijd.

Een muur is een eenvoudige constructie om de derde wet van Newton te illustreren. De muur oefent een kracht uit op de grond, en de grond oefent eenzelfde, tegengestelde  kracht uit op de muur. Hoe groter de muur, hoe groter de kracht, dat lijkt logisch. Want grotere muren zijn zwaarder, ze wegen meer. Die kracht is echter niet enkel de verdienste van de massa van de muur, maar evenzeer speelt de massa van de aarde hierin een rol. Eenzelfde muur op de maan, zal minder wegen.

muur 3de wet newton

Om de puntjes op de i te zetten zullen we hier nog eens de begrippen massa en gewicht door de mangel halen. Massa is onafhankelijk van het zwaartekrachtveld. Ook zwevend in de ruimte heb je een welbepaalde massa, maar aangezien er geen zwaartekracht is, heb je geen gewicht. De massa wordt uitgedrukt in kg, waar je ook heengaat blijft dit onveranderlijk. Het is echter de valversnelling die ervoor zorgt dat deze massa een welbepaalde kracht zal ondervinden die gelijk is aan de massa van het voorwerp vermenigvuldigt met de valversnelling: F=mg. Je zou vanaf nu heel logisch je gewicht in Newton (eenheid van kracht) kunnen uitdrukken, maar het is niet gegarandeerd dat hiervoor een sociaal draagvlak is…

Hoe kijkt een bouwkundige nu naar die muur? Een bouwkundige onderscheidt zich in alle bescheidenheid van de andere stervelingen op deze aardbol met het sublieme en tevens subtiele inzicht dat de interactie tussen de muur en de grond evengoed moet gelden voor de interactie tussen de rijen stenen van de muur. Steunen de bovenste 3 rijen immers niet op alle onderste stenen? Waar men ook een snede neemt geldt de derde wet van Newton! Het spreekt voor zich dat de snede-kracht in de onderste rij van de muur groter is dan de snede-kracht in de bovenste rij. En in feite is dat al een structurele analyse van de muur voor het belastinggeval van z’n eigen gewicht. Voor complexere structuren zoekt men ook de snedekrachten voor elke mogelijke snede van de structuur en de derde wet van Newton vertelt ons dat we in elke snede wederkerige krachten moeten vinden tussen deel A van de constructie aan de ene kant van de snede en deel B aan de andere kant van de snede.muur 3de wet newton

Kortom: we snijden in gedachten eender welke constructie doormidden en gaan op zoek naar de snedekrachten. Helaas is het niet zo simpel, want krachten bestaan in feite niet in de realiteit. Een straffe uitspraak, I know, maar het wordt helemaal duidelijk in het volgende deel ‘over structuren’.

Even grote en tegengestelde groeten,

T.E.

cartoon dikker en dikker 2

 

 

 

Geplaatst op door Tijs Essel · 1 reactie

Ook voor Coronavirus-data geldt dat een getal meestal begint met het cijfer 1, 2 of 3, de wet van Benford volgend

Als je de lijst van Corona-besmettingen per land overloopt valt het je niet meteen op, maar de meeste getallen beginnen met 1, 2 of 3. En dat is toch bizar, want we hebben toch 9 mogelijkheden voor het eerste cijfer, met bijhorende kans van 1 op 9 (11%) Klopt niet. En er is meer: bijna alles om ons heen volgt deze wetmatigheid: de kans dat een getal begint met ‘1’ is 30%, de kans op een 9 slechts een kleine 5%. Neem maar de proef op de som en turf de getallen in je krant: je zal zien dat meer dan de helft van de getallen start met 1, 2 of 3. Ik vind dit waanzinnig! Het is de fysische wereld die spartelt in het keurslijf van ons positiestelsel.

2020-03-08 09_29_53-Benford.xlsx - Excel

Ik poneerde dit gisteren bij een vriend en we namen samen de proef op de som: we namen de krant en ik turfde het aantal keer dat een getal met een bepaald cijfer begon. En na enkele pagina’s van De Tijd doorploegd te hebben op zoek naar getallen was het overduidelijk: hoe hoger het cijfer hoe minder kans dat het een startcijfer is. Hieronder de uitslag waaruit overduidelijk blijkt dat de kans op het eerste cijfer niet gelijk verdeeld is.

turven De Tijd

We hebben daarna zowel het aantal inwoners als de oppervlakte van elk land op de zelfde manier geanalyseerd en we komen tot de zelfde verrassende vaststelling dat het cijfer 1 het meest voorkomt of het nu gaat over een aantal inwoners of een oppervlakte. Het maakt zelfs niet uit in welke eenheid de oppervlakte wordt beschouwd vierkante km, vierkante mijl, hectares,… de uitkomst zal eenzelfde beeld geven.

opp inwoners per land - benford

Ook ik vond dat op het eerste zicht verrassend en zelfs verbluffend: hoe is het mogelijk? Het fenomeen blijkt beschreven te zijn door de wet van Benford, en dat is wat wikipedia ons vertelt:

“De wet van Benford beschrijft de frequentieverdeling van het begincijfer van getallen in grote dataverzamelingen waarin een beperkte mate van stochasticiteit optreedt. De wet van Benford werd in 1881 ontdekt door de Amerikaanse wiskundige en astronoom Simon Newcomb, maar kreeg grote bekendheid door de herontdekking en publicaties in 1938 van Frank Benford, een fysicus die zijn hele leven bij het Amerikaanse bedrijf General Electric heeft gewerkt.”

De wet van Benford drukt op volgende wijze uit wat de kans is op een startcijfer ‘d’:

Toegepast op het cijfer ‘1’ geeft dit:

d 1 2 3 4 5 6 7 8 9
kans (%) 30,1 17,6 12,5 9,7 7,9 6,7 5,8 5,1 4,6

Hoe kunnen we dit verklaren? Er lijkt niet echt een eenvoudige wiskundige verklaring te zijn. Wat we wel kunnen aantonen is dat als we een frequentieverdeling beschouwen van de startcijfers die onafhankelijk moet zijn van de gebruikte eenheid, we op een logaritmische frequentieverdeling komen, zoals hierboven beschreven.  Concreet wil dat zeggen dat we er van uitgaan dat de eenheid voor bepaalde grootheden geen invloed heeft op het resultaat. Want het is de mens die heeft uitgevonden hoelang een meter is. Daar kan de natuur of de werkelijkheid der dingen zich niets van aantrekken.

Eens je beseft dat het switchen van de ene eenheid naar een andere in feite een vermenigvuldiging is, kan je het fenomeen begrijpen door er een cirkelvormige rekenlat bij te halen. Jammer genoeg heb ik er geen in bezit, maar op een Breitling Navitimer zijn de buitenste rijen getallen die je kan verdraaien ten opzichte van elkaar eigenlijk een rekenlat. Wat kan je daarmee doen? Getallen vermenigvuldigen door te draaien, zie ook: De geheimen van grootvaders rekenlat. Graag breng ik je aandacht op het feit dat meer dan de helft van de cirkel getallen zijn die beginnen met een 1, 2 of 3. Dus hoe meer we willekeurige getallen gaan vermenigvuldigen hoe meer we zullen voldoen aan de wet van Benford. En we moeten hierbij ook opmerken dat we meeste natuurwetten gebaseerd zijn op een vermenigvuldiging, denk maar aan F=ma, de gravitatiewet, wetten van Maxwel,…

Breitling-Navitimer-Rattrapante.--600x406

Een test die je eenvoudig zelf kunt doen is willekeurig gekozen getallen A, B en C vermenigvuldigen op een rekenmachine en turven wat de frequentieverdeling is van uitkomst AxBxC, en na een tijdje zal de wet van Benford zich aan je openbaren: cijfer 1 zal beduidend meer voorkomen dan de andere cijfers.

Geldt de wet voor alle reeksen van getallen? Nee, dat ook weer niet. Om dergelijke verdeling te hebben moeten de gegevens over meerdere grootte-ordes gespreid zijn. Dus de lengtes van personen vallen hier bijvoorbeeld niet onder. Ook een lijst van hoogste bergtoppen niet, maar een lijst van alle bergen op aarde dan weer wel.

Het is contra-intuïtief omdat het het begrip ‘ad random’ een beetje op z’n kop zet. Als je getallen door een computer ad random laat bepalen dan zullen ze niet aan de wet van Benford voldoen. Het zijn dan ook geen werkelijke dingen die gemeten of geteld kunnen worden, maar enkel een getal genomen uit een verzameling van getallen, zoals een lotto-trekking. Als je op een bepaald moment een aantal gegevens moet verzinnen, b.v. facturen of in een wetenschappelijk onderzoek, kan je maar beter zorgen dat deze voldoen aan de wet van Benford. Want je zou niet de eerste fraudeur zijn die tegen de lamp loopt doordat z’n data zo verzonnen is dat alle startcijfers gelijk verdeeld voorkomen.

Tot slot terug naar het Corona-virus. Een prachtig voorbeeld van exponentiële groei in de huidige fase. Zie ook: Dromen over het getal e. Wanneer je een bedrag laat opbrengen op de bank zal het totaal bedrag groeien. Maar om van 100 euro naar 200 euro te groeien moet het bedrag verdubbelen (groei: 50%), maar daarentegen om te groeien van 800 euro naar 900 euro hoeft het bedrag maar te groeien met 12,5%. Daarom blijft het totaalbedrag langer ‘hangen’ tussen 100 en 200 euro en groeit het sneller door van 800 naar 900 euro. Wat we terugvinden in de frequentieverdeling van alle bedragen die op de bank staan, daarvan zal 30% ook starten met een ‘1’ ! Ook voor het aantal Corona-besmettingen is het een verdubbeling om van 1000 naar 2000 besmettingen te gaan, maar slecht een kleine groei om van 8000 naar 9000 besmettingen te gaan. En dat raakt volgens mij de ziel van deze mooie wetmatigheid.

Getallen die de Benford-wet volgen zijn echt en staan met beide voeten in de werkelijkheid.

Het is op dit moment (begin maart 2020) nog koffiedik kijken hoeveel het maximale aantal besmettingen per land zal zijn, maar één ding weten wel wel: het zal voldoen aan de wet van Benford.

En in tijden van onzekerheid, is dit misschien een lichtpuntje.

Benford-verdeelde groeten aan iedereen,

T.E.

Geplaatst op door Tijs Essel · 3 reacties

Tijd voor een spelletje Dobble! Maar wacht eens… hoe zit dat in elkaar?

Dobble. Zeggen dat je zenuwen gesloopt worden is misschien overdreven, maar je zenuwen worden toch serieus onder druk gezet. (Zoveel bouwkundige uitdrukkingen in ons dagelijks leven waar je op kunt bouwen!) Je hebt kaarten met daarop 8 verschillende symbolen en elke twee kaarten hebben slechts één gemeenschappelijk symbool. En dat moet je natuurlijk zo snel mogelijk in de mot hebben om te winnen. En kinderen kunnen er verduiveld goed in zijn. Maar wacht eens even… stel dat je meer of minder symbolen per kaart hebt… papa moet even iets gaan opzoeken, meisjes!

dobble

En ja… net wat ik dacht. Er bestaat een formule dat aangeeft wat het maximale aantal kaartjes is dat je kan maken met een bepaald aantal symbolen op je kaart. Voor een zeer eenvoudig geval van 2 symbolen per kaart kan je gemakkelijk uitzoeken dat het maximaal aantal kaarten 3 is. Stel dat de symbolen A, B en C zijn, dan zul je 3 kaartjes hebben: AB, AC en CB. Ieder kaartje heeft inderdaad slechts één gemeenschappelijk symbool. We kunnen dus al stellen dat 2 symbolen –> 3 kaartjes. Hieronder een grafiek waarop de kaartjes zijn weergegeven en de lijnen tonen aan welke symbool de kaarten gemeenschappelijk hebben.

IMG_20200207_0004

De grafiek heeft de volgende eigenschappen (lijnen staan voor symbolen, kaarten zijn de snijpunten):

  • Gelijk welke twee kaarten zijn telkens verbonden met één lijn (dat zorgt er voor dat er tussen elke twee kaarten een gemeenschappelijk symbool is)
  • Gelijk welke twee lijnen snijden slechts in één kaart (zorgt ervoor dat er slechts één gemeenschappelijk symbool is)

So far so good, maar wat met 3 symbolen per kaart? Hoeveel verschillende symbolen en dus hoeveel kaarten kan je nu maken? Laten we maar direct proberen een grafiek te maken waar elke kaart het kruispunt is van 3 lijnen (3 symbolen per kaart)… In de grafiek staan 4 kaarten en we maken gebruik van 6 symbolen A tot F.

IMG_20200207_0005

Maar we kunnen met 3 symbolen verder gaan dan 4 kaarten, hieronder een grafiek van het maximaal mogelijke aantal kaarten met 3 symbolen. Ook hier geldt dat alle twee kaarten verbonden zijn met een lijn, en dat 2 lijnen slechts op één punt snijden. En inderdaad, niemand zei dat het rechte lijnen moesten zijn hé. Vervang de letters door leuke tekeningen en je kan al een zeer eenvoudige Dobble-spel samenstellen van 7 kaarten met telkens 3 symbolen op de kaart.

IMG_20200208_0001

Dus met 2 symbolen per kaart vinden we een maximum van 3 kaarten en 3 verschillende symbolen. En met 3 symbolen vinden we maximum 7 kaarten en 7 verschillende symbolen: ABC, CFG, CDE, BEG, AEF, BDF en ADG. Het spreekt misschien iets meer aan met echte symbolen en mooie kleurtjes:

fano-plane.png

Het kan wiskundig aangetoond worden dat als we r symbolen per kaart kiezen het totaal aantal kaarten N (en ook het totaal aantal verschillende symbolen) gelijk is aan:

Dit lijkt inderdaad te kloppen voor r=2, dan wordt N=3. Bij r=3 vinden we dat N gelijk is aan 7. Deze ‘Dobble’-formule blijft geldig voor hogere waarden van r. Maar het maken van de grafiek wordt dan steeds wat complexer. stel nu dat we r=4 nemen, dan krijgen we een totaal van N=13, een bijhorende grafiek vind je hieronder. De zwarte punten staan voor de 13 kaarten en de 4 lijnen die er snijden stellen de symbolen voor, hier voorgesteld als 13 verschillende kleuren.

SymmetricalProjectivePlaneOrder3

En zo kunnen we verder gaan en voor r=5 vinden we N=21.

21lines

En voor 8 symbolen per kaart, zoals bij het Dobble-spel vinden we N=57. Ook hiervan heb ik een grafische weergave gevonden, je kan zien dat voor kaart 1 helemaal in het midden er 8 lijnen samenkomen.

pporder7

Maar wat merken we op als we de kaarten van Dobble tellen? Weliswaar 57 verschillende symbolen, maar slechts 55 kaarten! Dit wil zeggen dat er nog 2 unieke kaarten kunnen aangevuld worden aan het spelletje Dobble. Welke precies? Daar ben je ook al snel een avondje mee zoet denk ik.

Waarom 55 kaarten en niet 57? Dat is geen complot of vergetelheid denk ik, maar gewoon optimalisatie bij het drukken. Bij een gewoon spel speelkaarten stel je ook vast dat er naast de 52 kaarten (13×4) ook nog 2 jokers bijzitten en nog een instructie-kaart, wat het totaal brengt op 55 kaarten, die netjes in 11 rijen van 5 kaarten voorbij zoeven in de drukkerij… Ja, we eindigen gewoon met boerenverstand en de tafel van 5.

Tot zover een spelletje Dobble spelen met papa…

Aan iedereen unieke groeten,

T.E.

 

Geplaatst op door Tijs Essel

Priemgetallen staan in voor uw veiligheid… voorlopig althans

In 1977 werd door de heren Ron Rivest, Adi Shamir en Len Adleman een asymmetrisch encryptiealgoritme (de RSA encryptie) ontworpen , dat gebaseerd is op het ontbinden in factoren van grote getallen. Het is namelijk zeer gemakkelijk om getallen te vermenigvuldigen, maar het duurt eeuwig om deze getallen opnieuw te ontbinden in z’n factoren. Als deze twee getallen priemgetallen zijn dan is er maar één ontbinding mogelijk. Het is een mooi voorbeeld van hoe op het eerste zicht nutteloze wiskunde (de zoektocht naar zeer grote priemgetallen) toch de mensheid ten dienste kan zijn. De afkorting RSA is afkomstig van Rives-Shamir-Adleman: hieronder vrolijk samen op een graspleintje.

RSA

Wie al eens het moedige idee gehad heeft om een puzzel van meer dan duizend stukjes in elkaar te puzzelen zal beamen dat het proces van duizend stukjes naar puzzel veel langer duurt dan wanneer je op het einde de puzzel omzet naar duizend stukjes en de hele poespas weer in de doos kiepert in afwachting tot iemand anders op het idee komt om de stukken terug samen te puzzelen tot één of andere Oostenrijkse bungalow met een overdaad aan bloemen. Althans zo herinner ik me dergelijke puzzels. Hetzelfde geldt voor het ontbinden van het product van twee grote priemgetallen. Je kan in een fractie van een seconde het product maken, maar de ontbinding duurt jaren, en dat principe is zeer handig om een asymmetrische versleuteling te ontwerpen.

Wanneer ik mijn huis verlaat gebruik ik een sleutel om naar buiten te gaan. Wanneer ik na een tijdje weer naar binnen wil gebruik ik diezelfde sleutel. Het feit dat we voor beide richtingen (naar buiten en naar binnen) dezelfde sleutel gebruiken zorgt ervoor dat we in een symmetrische situatie zitten. Wanneer je echter een andere sleutel zou nodig hebben om weer naar binnen te komen dan is er sprake van asymmetrie. Zo’n systeem heeft meestal een publieke sleutel en een privé sleutel. Een publieke sleutel betekent dat iedereen de manier weet om een boodschap te versleutelen, maar dat alleen de ontvanger de manier weet om die versleutelde boodschap terug te brengen naar de oorspronkelijke boodschap.

Een uitleg over encryptie kan in feite niet zonder Alice en Bob op te trommelen die een boodschap willen uitwisselen, die niet onderschept mag worden door Eve! Bij een asymmetrische encryptie zal Bob een publieke sleutel aan Alice geven waarmee zij een boodschap kan versleutelen. Doordat deze sleutel publiek is kan Eve deze sleutel onderscheppen, maar ze kan deze sleutel niet gebruiken om de boodschap te ontcijferen. Dat kan alleen Bob, want hij beschikt over een private sleutel die hij met niemand heeft gedeeld, waarmee hij de boodschap kan decoderen. Superhandig want Alice en Bob kunnen zonder geheime sleutels aan elkaar te geven toch boodschappen uitwisselen, die Eve niet kan ontcijferen. In feite moet ik zeggen: nog niet kan ontcijferen…

Alhoewel de RSA-versleuteling met de huidige snelheid van traditionele computers bijna onmogelijk gebroken kan worden omwille van de enorme rekentijd die nodig is om een zeer groot getal te ontbinden in factoren, is het niet ondenkbeeldig dat er in de toekomst wel degelijk manieren zullen gevonden worden om de RSA-versleuteling toch te kunnen breken. Kwantumcomputers zouden over een paar jaren de klus kunnen klaren in enkele uren waar de klassieke computers eeuwen voor nodig hebben.

Dan kunnen we al vermoeden wat de de geheime informatiediensten van veel landen aan het doen zijn: massaal veel data in z’n versleutelde toestand opslaan totdat het moment komt dat de kwantumcomputers ver genoeg ontwikkeld zijn en er een algoritme zal gevonden worden worden om op relatief korte tijd zeer grote getallen te kunnen ontbinden… Hoog tijd dat er een andere ogenschijnlijk onnuttige tak van de wiskunde van het rek wordt gehaald om een nieuwe manier te vinden om boodschappen te versleutelen.

Gedecodeerde groeten,

T.E.

 

 

Geplaatst op door Tijs Essel · 1 reactie

Het theorema van Bayes en de NIPT-test

In de EOS van september 2019 las ik de column ‘Nipte cijferverwarring’ van Hetty Helsmoortel over de NIPT-test, een test om een Down-zwangerschap op te sporen. Zonder hier evenwel in te gaan op het maatschappelijk debat over deze NIPT-test, is het een mooi voorbeeld over het verrassende karakter van de uitkomst van het theorema van Bayes. Anders dan bij Hetty zullen we hier even dieper ingaan op de toepassing van Bayes, en wellicht zal er ook een formule tevoorschijn komen. Hopelijk zien we elkaar op het einde van dit stukje terug, en ben je niet blijven haperen aan de formule.

Nipte cijferverwarring

Update. Zo zou je het theorema van Bayes met één woord kunnen samenvatten. Er is een gebeurtenis waardoor je kennis over iets een update krijgt. In het geval van de NIPT-test heb je als zwangere vrouw een bepaalde kans op een Down-zwangerschap, dat wordt de a-priori-kans genoemd. De NIPT-test heeft uiteraard als doel om uitsluitsel te krijgen over een Down-zwangerschap, maar helaas brengt deze geen 100% zekerheid, maar het zal de kennis over de waarschijnlijkheid wel sterk verhogen, en resulteren in een a-posteriori-kans.

Een feilloze test zou je in één klap zekerheid bieden. Een positieve test zou betekenen dat de kans op een Down-zwangerschap 100% is, en wanneer je negatief test zou het uiteraard ook helemaal zeker zijn dat er geen Down-zwangerschap is. Maar helaas bestaat zo’n test niet. Wat betref de NIPT-test heb je 99,2% kans dat je postief test bij een Down-zwangerschap, dat wordt de sensitiviteit genoemd. Het is de kans op een postieve test (POS) op voorwaarde dat er een Down-zwangerschap is (D), de voorwaardelijke kans wordt als volgt uitgedrukt, waarbij P staat voor probability:

P(POS|D)=0,992

Bij een voorwaardelijke kans kan je niet zomaar de argumenten omdraaien. De kans op een positieve test gegeven een Down-zwangerschap is niet hetzelfde als de kans op een Down-zwangerschap gegeven een postieve test. Zo is bijvoorbeeld ook de kans op regenweer gegeven dat je een paraplu bij je hebt helemaal niet dezelfde als de kans dat je een paraplu bij je hebt bij regenweer.

De specificiteit van een test is de kans dat je negatief test gegeven dat er geen sprake is van een Down-zwangerschap. Bij de NIPT-test is de specificiteit 99,9%. Dat kan al volgt symbolisch uitgedrukt worden, waarbij G staat voor ‘geen Down-zwangerschap’:

P(NEG|G)=0,999.

Hieruit volgt logischerwijs dat er 1 kans op 1000 is dat je positief test terwijl je geen Down-zwangerschap hebt (ook wel soms omschreven als de vals-positieven), dit kunnen we noteren als:

P(POS|G)=0,001.

In de column ‘Nipte cijferverwarring’ wordt beschreven dat iemand bericht krijgt dat ze positief getest heeft. Wetende dat de specificiteit en de sensitiviteit van de test respectievelijk 99,9% en 99,2% is, percentages die toch flirten met de 100% lijkt het op het eerste zicht een certitude te zijn dat de betreffende persoon effectief een Down-zwangerschap heeft, maar verrassend genoeg stond in de brief dat de voorspellende waarde van de test 50% bedroeg gezien haar leeftijd. Hoe valt dat te verklaren?

Nu komt de Bayesiaanse aap uit de mouw! Zoals gezegd heb je als je geen Down-zwangerschap hebt toch één kans op duizend dat je positief test (de vals-positieven, afgeleid uit de specifiteit van de test). Hoog tijd om een cruciaal ontbrekend element boven water te halen. Welke absolute kans is er op een Down-zwangerschap? We weten dat deze kans toeneemt met de leeftijd, voor personen tussen 25 en 30 jaar is deze kans 1 op 1000, bij hogere leeftijden loopt dit op tot een kans van 12 op 1000. Zonder formules kunnen we dus wel al zien dat de kans op een Down-zwangerschap bij pakweg 27 jarigen van dezelfde grootte-orde is als de kans op een vals-positieve test. En dat betekent inderdaad dat de kans op een Down-zwangerschap gegeven een positieve test ca 50% bedraagt.

Nu komt het moment om er toch even de formule van Bayes bij te halen, zodat het plaatje compleet wordt, de formule zal de kans geven op een Down-zwangerschap bij een positieve test P(D|POS) en we weten ondertussen dat dit geheel iets anders is dan de kans op een positieve test bij een Down-zwangerschap P(POS|D). Want ontvang je een positieve test dan ligt je interesse uiteraard bij P(D|POS), deze voorwaardelijke kans wordt als volgt berekend:

We merken op dat de formule van Bayes onderzoekt welk aandeel de correcte positieve testen heeft ten opzicht van alle positieve testen P(POS). De noemer geeft de kans weer op alle positieve testen, los van al dan niet aanwezigheid van een Down-zwangerschap, dit is een optelling van de kans op een correct positieve test P(POS|D)P(D) en de kans op een vals positieve test P(POS|G)P(G), wat leidt tot de volgende uitdrukking:

Gezien alle argumenten van het rechterlid gekend zijn, kunnen we de bovenstaande uitdrukking evalueren om de kans te ontdekken op een Down-zwangerschap gegeven een positieve NIPT-test:

Om het helemaal helder te maken kunnen we een tabel opstellen voor 1 miljoen personen, die zwanger zijn en behoren tot de leeftijdsklasse 25-30 jaar:

tabel bayes

Uit deze tabel zie je dat van alle 1991 postieve testen, er 999 vals-positief zijn. En dat de kans op een Down-zwangerschap bij een postieve test dus 992/1991=0,498… is.

En hier zien we dus inderdaad dat deze kans ca. 50% bedraagt. Misschien op het eerste gezicht verrassend, maar na het lezen van dit stukje hopelijk een stuk helderder.

Specifieke, maar ook zeer sensitieve groeten,

T.E.

Geplaatst op door Tijs Essel · 1 reactie

Er was eens een appel. Hap. Op.

Pavlovgewijs komt bedtijd bij kleuters meestal samen met de vraag om een verhaaltje. Het kan wel eens gebeuren dat de tijd ontbreekt om hier uitvoerig op in te gaan en dan wordt door ondertekende het volgende ‘kortverhaal’ wel eens bovengehaald: “Er was eens een appel. Hap. Op.” Ik krijg dan prompt een ontgoocheld dat-is-geen-echt-verhaal-gezicht te zien, en nog voor ik de kamer helemaal verlaten heb, maken zich, naast een schuldgevoel, ook echte verhalen over appels meester van m’n gedachten.

hendrick_de_clerck_the_judgement_of_paris.jpg

Zo is er het verhaal over de twistappel van Eris, godin van de ruzie. Zij was ooit te gast op een huwelijksfeest waarop ook tal van Griekse goden aanwezig waren. Ergens tussen de ‘Lac de Connemara’ en ‘YMCA’ pakte ze een appel van het dessertbuffet en schreef erop: ‘Voor de mooiste’ en legde die netjes terug tussen het andere fruit van het buffet. Dat Griekse goden wel af en toe menselijke trekjes hadden was al langer duidelijk, maar die avond liep het echt de spuitgaten uit. Het duurde niet lang of drie godinnen, Hera, Pallas Athena en Aphrodite, maakten zo’n scène over wie de appel toekwam dat Zeus in hoogsteigen persoon moest ingrijpen. Hij stelde de Trojaanse prins Paris als scheidsrechter aan.

Deontologie en integriteit waren niet meteen de sterkste kanten van Paris, want nadat Hera en Athena hem respectievelijk macht en wijsheid beloofden ging Paris in op het voorstel van Aphrodite. In ruil voor de appel en de titel van mooiste godin beloofde ze hem de mooiste vrouw van de toen bekende wereld: Helena. Haar man, Menelaos, was not amused en zo begon de Trojaanse Oorlog die leidde tot de val van Troje, met behulp van een houten paard dat ‘geschonken’ werd aan de Trojanen. De Trojanen liepen blindelings in de val ondanks de waarschuwing van de plaatselijke hogepriester Laocoön: “Timeo Danaos et dona ferentes.” Ik vrees de Grieken, en vooral als ze met cadeautjes afkomen. Ook vandaag nog wordt dit her en der gemompeld als iets te mooi is om waar te zijn. In 90% van de gevallen is het meestal ook zo. Het was niet zo handig van Aphrodite om Paris een getrouwde vrouw te beloven. Het is alsof je iemand een Porche zou beloven die je niet zelf bezit. Of een volk een land zou beloven waar andere volkeren reeds wonen. En dat is precies wat gebeurde in het Oude Testament.

De-zondeval

De appel speelde ook een hoofdrol in het Genesis-verhaal van het Oude Testament. Jahweh, het welbekende hoofdpersonage, had z’n versgeschapen koppeltje mensen, Adam en Eva, verboden de vruchten van de boom van goed en kwaad te eten. Het feit dat in het Latijn het woord ‘malus’ zowel ‘slecht’ als ‘appel’ betekent, zal wellicht een verband hebben met het feit dat het een appelboom betrof. Een slang overtuigde Eva tot een hap, en even later verslikte Adam zich bij z’n laatste hapje appel toen hij hoorde over de erfzonde die ze zo hadden uitgeroepen over hun volledige nageslacht. Oeps.

De slang, de veroorzaker van al dit onheil, was, naar verluidt, niet zo onder de indruk van z’n bestraffing welke erin bestond dat z’n nageslacht voortaan al kruipend door het leven moet gaan en moest zelf inspanning doen om een opkomende glimlach te onderdrukken. Ook Adam en Eva kregen een straf voor hun nageslacht. Vanaf dan zouden mannen zich in het zweet moeten werken op de akkers en zouden vrouwen pijnlijk bevallen. Waarbij ik moet vaststellen dat het grootste deel van de mannen ondertussen bezigheden heeft gevonden in andere sectoren dan de agrarische sector, maar dat vrouwen daarentegen nog altijd een serieuze klus hebben met de bevalling. Wat zou er van ons geworden zijn mochten we geen kennis genomen hebben van de boom der kennis van goed en kwaad via die ene appel? We zullen het nooit weten…

Newton appel

En het is ook een appel die de natuurkundige Isaac Newton inspireerde tot z’n zwaartekrachtswetten. Hij kwam tot het geniale inzicht dat planeten dezelfde wetten volgen als die vallende appel. Niets zo logisch als de wetten van Newton? Toch niet want onlangs was ik met m’n collega’s bezig over een vallende lift en de snelheid waarmee deze de grond raakt. Een collega kon amper geloven dat een lift vol met mensen precies met dezelfde snelheid tegen de grond valt als een lege lift. De volle lift en de lege lift vallen immers naar beneden met dezelfde versnelling, de valversnelling. En omdat de luchtweerstand van beide situaties gelijkaardig is, zal de snelheid identiek zijn.

Nog niet zo lang geleden reed ik met mijn dochter in de auto en ze vloog naar rechts bij een rond puntje. ‘Hoe komt dat toch papa?’ En voor ik het besefte ging ik op m’n rem staan om te tonen dat er ook bij vertragen en versnellen krachten op ons inwerkten. En puur educatief ging ik wat sneller door het volgende ronde puntje om te tonen dat de zijwaartse krachten dan groter zijn. Ik was zo enthousiast de eerste en de tweede wet van Newton aan het uitleggen dat ik per abuis ook bijna de derde wet over actie en reactie had uitgelegd ten nadele van een voorligger.

GPS

Dat doet me denken aan een andere appel: de Apple Iphone. En meer specifiek de GPS functie. En bij uitbreiding natuurlijk alle GPS-toestellen. Die zouden allen compleet de mist ingaan enkel maar vertrouwend op Newton’s wetten, want de klokken in de satellieten gaan sneller dan de klokken op aarde, dat is een gevolg van de relativiteitstheorie van Einstein die geldt als een correctie op de wetten van Newton. Het hele satellietsysteem kan je eigenlijk vergelijken met geblinddoekt rondlopen en een aantal personen die tegen je roepen hoe laat het is en waar ze zelf staan. Doordat je zelf weet hoe laat het is, weet je hoe lang het geluid er over gedaan heeft om je te bereiken. Als één iemand roept dat hij op de kerktoren staat en roept dat het ‘nu’ 12u is, en je hoort de ‘nu’ pas 12u en 2 seconden. Dan weet je dat je je ergens op een cirkel van 600 m rond die kerk bevindt (meer exact op een bol van 600m gemeten vanop de kerktoren). Heb je 3 van die roepers, dan kan je in theorie perfect je positie bepalen. Zo heb je minstens 3 satellieten nodig om je plaats op aarde te bepalen.

Ja, je plaats op aarde. Iedereen is er vroeger of later naar op zoek. En we komen er al snel achter dat er veel meer nodig is dan 3 satellieten om je plaats te vinden op aarde. Gelukkig hebben we verhalen over appels die ons een beetje op weg helpen over hoe alles ineen steekt want voor je het weet: ‘Hap. Op’. Ik denk dat ik maar eens meer tijd moet vrijmaken voor slaapverhaaltjes… Volgende keer Sneeuwwitje!

Appelbloesemgeurige groeten,

T.E.

sneeuwwitje

Geplaatst op door Tijs Essel · 1 reactie

Bladschikken voor gevorderden met de gulden snede

De gulden snede staat al eeuwen bekend als de perfecte esthetische verhouding. Er zijn heel wat gebouwen die volgens deze perfecte ratio gebouwd zijn. De Taj Mahal, het Parthenon, de Notre Dame in Parijs, overal zie je de gulden snede terugkomen. Maar wat wonderlijk is, is dat deze gulden snede ook in de natuur terugkomt. Bij veel planten en bloemen zijn de blaadjes geschikt volgens de gulden hoek, wat het equivalent is voor de gulden snede bij hoeken.

1-NGNon6GsqrUSrzMsF9vrEw

Mijn trans-Alpijnse zus heeft zonet een boek gelezen over de gulden snede: ‘La sezione aurea’. In het Italiaans klinkt dat zoveel mooier dan in het Nederlands, waar ‘gulden’ klinkt alsof het gaat om iets dat wat verguld is en kitsch, en snede is iets wat wij hier vooral associëren met een snee brood of het sneetje kaas dat we erop leggen. Een kitcherige boterham. Weg mystiek.

De gulden snede is de verhouding van twee lijnstukken waarbij het grootste zich verhoudt tot het kleinste, zoals de som van beiden zich verhouden tot het grootste lijnstuk.
Golden-Ratio-color-1024x439-1.png

Hieruit volgt de volgende uitdrukking:
Beide leden vermenigvuldigen met geeft de volgende kwadratische vergelijking:

met als positieve oplossing:

Een benaderende waarde voor de gulden snede is dus 1,618.

Mijn zus was vooral verwonderd over het verband tussen de gulden snede en de fyllotaxis. Dat heb ik toch eens moeten opzoeken, en dat blijkt de schikking van de blaadjes te zijn. Bladschikking blijkt voor planten van primordiaal belang te zijn. De fotosynthese is een proces waarbij licht moet opgevangen worden om koolstofdioxide (ook wel gekend als C02) om te zetten in koolhydraten. Een plant heeft er dus alle belang bij om z’n blaadjes zo te schikken dat ze zoveel mogelijk licht opvangen, en dat met een zo gemakkelijk mogelijke opdracht. In de DNA zou ergens kunnen de volgende opdracht weggeschreven zijn: schik het volgende blaadje onder een hoek  van het vorige blaadje.

Wat zou die hoek kunnen zijn? Als we =180° nemen, zien we al snel dat dit helemaal geen goede keuze is, want het derde blad komt boven het eerste blad te liggen. Ook 120° is geen goed idee, want na drie blaadjes ligt het vierde knal op het eerste blaadje, wat uiteraard niet efficiënt is voor de fotosynthese van de plant. We merken dat alle getallen die een gemakkelijke breuk vormen (360°/180°=2 en  360°/120°=3) geen goede oplossing zijn voor de bladschikking. Bij uitbreiding zijn alle rationele getallen vroeg of laat overlappend met vorige geschikte blaadjes. We zoeken dus een getal dat zich zo irrationeel mogelijk gedraagt.

Misschien is een goede keuze? Nee, want 22/7=3,142.. is al een zeer dichte benadering. Dat wil zeggen dat al veel te dicht aan het flirten is met de rationele getallen om bruikbaar te zijn voor een nuttige bladschikking. Dit kan men goed zien als we de enkelvoudige kettingbreuk van uitzetten:
Als we de kettingbreuk afbreken bij 7 dan krijgen we de verhouding 22/7. Hele grote getallen zorgen in een kettingbreuk voor een goede benadering met rationele getallen. Zo is 355/113=3.14159292… een zeer goede benadering voor . Dit komt omdat het volgende getal in de kettingbreuk een heel groot getal is: 292.

Als grote getallen in een kettingbreuk leiden tot getallen die zich gemakkelijk laten benaderen door een rationeel getal, kunnen we dus ook omgekeerd zeggen dat een kettingbreuk met kleine getallen zal leiden tot een zeer irrationeel getal. En het meest irrationele getal dat we kunnen bekomen is een kettingbreuk met alleen maar eentjes:

Het zal je niet verwonderen dat deze uitdrukking in deze tekst die handelt over de gulden snede effectief perfect gelijk is aan de gulden snede:

Terug naar de plant met de DNA opdracht: schik de blaadjes volgens de gulden hoek. De gulden hoek wordt uitgedrukt als:

Dat is de kleinste hoek van twee hoeken die een volledige cirkel verdelen in twee hoeken volgens de gulden snede: 137,5°+ 222,5°=360° en 222,5/137.5=1,1618…

Hieronder zie je de eerste 5 blaadjes van een plant geschikt volgens de gulden snede, de blaadjes bevinden zich telkens een hoek 137,5° verder van elkaar. Of 222,5° in tegenwijzerzin.

Leaf-Growth-5.png

Zo gaat het door en door en we verkrijgen telkens een zo minimale overlap met de vorige blaadjes.

Leaf-Growth-13.png

Ook bij de schikking van de zaadjes in een zonnebloem gebeurt iets gelijkaardig. De zaadjes zijn allemaal geschikt volgens de gulden hoek. Dit levert immers de meeste zaadjes op een zo klein mogelijke oppervlak op. Hieronder kan je zien dat een kleine variatie van de hoek al een veel minder gunstige schikking oplevert van de zaadjes.Sunflower-seed-golden-angle-diagram.001.pnglabimg_870_Sunflower

Als je je nu de bedenking maakt: amai hoe kan dat? Dan moet je maar denken aan het feit dat alle minder gunstige variaties in de natuur met minder gunstige hoeken het niet hebben overleefd ten opzichte van de planten met een gunstigere schikking. Wat we in de natuur vinden is het product van een proces van miljoenen jaren variatie, overerving en selectie. (lees ook: Hoe intelligent is de hemelse horlogemaker?) Je zou het sommige mensen niet aangeven, maar ook die zijn het product van miljoenen jaren van finetuning.

Oh ja en dan hebben we ook nog de wonderbaarlijke Fibonacci getallen: 1,1,2,3,5,8,13,… waarvoor geldt dat het volgende getal telkens de som is van de twee vorige getallen. Er zijn in de natuur ook veel Fibonacci getallen te vinden… Mysterieus van de natuur? Helemaal niet want laten we eens de gulden snede benaderen door de kettingbreuk af te breken dan krijgen we volgende benaderingen:

Twee opeenvolgende Fibonacci getallen blijken dus een steeds betere benadering van de gulden snede te zijn naarmate we verder gaan in de Fibonacci rij:

De natuur vond immers ook dat, als we dan toch getallen of een verhouding gebruiken in het bladschikken of het zaadschikken,  we maar beter Fibonacci getallen kunnen gebruiken.

Je hoeft trouwens niet  met de eerste Fibonacci getallen 1 en 1 te starten om uit te komen op de gulden snede. Neem eender welke twee getallen en tel ze samen en maak dan telkens de som van de laatste twee getallen en je komt sowieso altijd uit op de gulden snede. Als je pakweg 37 en 11 neemt zal dit ook een reeks vormen waarvan de verhoudingen op de limiet de gulden snede zijn. Ik heb het niet nagegaan, maar het moet wel gewoon altijd lukken. Dat is niet echt een straf wiskundig bewijs, maar dat laat ik over aan anderen.

Nu ik erover nadenk. Net omdat de gulden snede het meest irrationele getal is dat we kunnen bedenken zal het waarschijnlijk totaal geen streling voor het oor zijn als we twee klanken zouden laten samenklinken waarvan de verhouding van de frequenties gelijk is aan de gulden snede. Want enkel eenvoudige verhoudingen van gehele getallen zijn harmonische tweeklanken. (zie ook: Alle piano’s zijn een beetje vals). Dat is toch wat anders dan je zou verwachten van deze sectio divina, of goddelijke verhouding.

We kunnen besluiten dat de gulden snede hoogstwaarschijnlijk leidt tot het meest irritante, dissonante en valse interval in de hele muziekwereld. Geen idee of dat ook in het boek van mijn zus stond. Ik hoor het wel binnenkort!

Zorgvuldig in het lente-zonlicht geschikte groeten,

T.E.

Geplaatst op door Tijs Essel · 1 reactie

De geheimen van grootvaders rekenlat

Om te rekenen hebben we tegenwoordig rekenmachines en smartphones ter beschikking, maar er is een tijd geweest, nog niet eens zo lang geleden, dat alle bewerkingen met getallen manueel moesten gebeuren. Met pen, papier en veel monnikengeduld geraak je wel ergens, maar in grootvaders tijd hadden ze als hulpmiddel een rekenlat. Ik vroeg me al lang af hoe zo’n ding werkt, en ik heb me er één aangeschaft, ter ontsluiering van z’n geheimen.

20190228_215417

Iedereen heeft wel eens twee kinderen horen bekvechten, waarbij de ene beweert wel duizend knikkers te hebben en waarbij de andere met hoongelach de andere duidelijk maakt dat hij er nog veel meer heeft: wel honderd! Waarbij knikkers inwisselbaar zijn in om het even wat, naargelang het onderwerp van de discussie. Het door elkaar haspelen van grootte-ordes is nu eenmaal hilarisch. Reeds in de lagere school leren we hoeveel nulletjes we moeten bijvoegen om een getal te vermenigvuldigen met honderd of duizend. Mijn dochter geeft me zonder verpinken de antwoorden: om met tien, honderd of duizend te vermenigvuldigen moet je respectievelijk één, twee en drie nulletjes toevoegen aan het getal. Zeer interessant want het vermenigvuldigen met veelvouden van 10 is dus in feite equivalent aan het optellen van nulletjes. We hebben dus van een vermenigvuldiging een optelling gemaakt…

Ik ben me er ter dege van bewust dat het optellen van nulletjes om tienduizend met pakweg een miljoen te vermenigvuldigen niet echt rocket science is, maar de dualiteit tussen optellen en vermenigvuldigen is het principe dat aan de basis ligt van de werking van een rekenlat. Er moet enkel nog een abstractiesausje over en het geheel moet nog wat gekruid worden met een ‘moeilijk woord’, maar het concept zal blijven dat we grootte-ordes van getallen optellen om ze te vermenigvuldigen. De bekvechtende kinderen van daarnet hadden het over grootte-ordes van tien. Honderd. Duizend. Miljoen. Miljard. En ga maar door… Het is duidelijk dat tien een centrale rol speelt in dit geval. De grootte orde van tienduizend is 4 en de grootte orde van een miljoen is 6. Het vermenigvuldigen van tienduizend en een miljoen is dus equivalent aan het optellen van de grootte ordes: 4+6=10.

Het abstractiesausje zullen we opdienen in twee gangen samen met twee vragen. De eerste vraag is: heeft elk getal een grootte orde? Affirmatief! Zoals je 10 kunt verheffen tot de 2de macht om 100 te bekomen, kan je perfect 10 verheffen tot de macht 2,5. Verheffen betekent letterlijk ‘naar een hoger niveau brengen’. Het antwoord op 10 tot de macht 2,5 is trouwens 316,227766… Het gaat alleszins serieus hard als we beginnen met verheffen, 10 tot de macht 80 is een schatting van het totaal aantal atomen in het heelal. We kunnen dus redelijk wat omspannen met 80 grootte-ordes van 10. Het aantal atomen in een mol: grootte-orde 23 (zie ook het stukje: Over een lepeltje, oceanen en moleculen). ‘Googol’ is de aanduiding voor de 100ste macht van 10, daar komt trouwens de naam Google vandaan.

Een ‘googolplex’ is 10 tot de macht googol, en we blijven ons wiskundehartje verheffen want een ‘googolplexian’ is dan weer 10 tot de macht googolplex. Letterlijk niet te bevatten want er zijn niet genoeg atomen in het heelal om te voorzien in alle nullen en ik kan dan ook met recht en rede zeggen dat dit ons veel te ver leidt. Als je nog harder wil gaan dan het machtsverheffen, moet je zeker eens zoeken (Googelen bijvoorbeeld) naar het ‘getal van Graham’.

De tweede vraag is: kan een ander getal dan 10 gebruikt worden als het grondtal voor de grootte-orde? En ook hier is het antwoord eveneens positief. Natuurlijk kan je dat. Het binair talstelsel is een mooi voorbeeld, waarbij het grondtal 2 is. (zie ook: Schaakmat voor koning Shirham) Maar waarom het gemakkelijk maken als het ook moeilijk kan? Waarom nemen we niet gewoon het grondtal e? (zie ook: Dromen over het getal e) Hiermee kunnen we zeer goed continue groei wiskundig omschrijven. En in de natuur zijn er nogal wat zaken die volgens dat principe werken, ik denk maar aan de afname van radioactiviteit. Als we e nemen als grondtal dan zal de x-de macht van e de continue 100%-groei weergeven in een tijdspanne x. Maar zoals we alle getallen kunnen uitdrukken als machten van 10 of 2, kunnen we evengoed alle getallen uitdrukken als een macht van e. Uiteraard mag dit niemand ervan weerhouden om nog een ander grondtal te nemen, gewoon om tegen tjok te zijn. (zie ook: De ontplooiing van het verhaal van ‘tegen tjok’ rolmodel Britney Gallivan).

Na deze flexibiliteit naar grootte-orde en naar grondtal, is het dringend tijd voor het kruiden van het geheel met een moeilijk woorden. We hebben steeds gesproken over de grootte-orde van een getal op basis van een grondtal. Zo is de grootte-orde van 1000 op basis van grondtal 10 gelijk aan 3. En is de grootte-orde van 16 op basis van grondtal 2 gelijk aan 4. Vanaf nu gaan we grootte-orde vervangen door ‘logaritme’. Laten we nu bovenstaande voorbeelden nemen dan zeggen we dat de logaritme met grondtal 10 van 1000 gelijk is aan 3. Notatie:

en de logaritme met grondtal 2 van 16 gelijk is aan 4. Notatie:

Meer algemeen geldt de volgende definitie:

Wanneer we als grondtal e nemen, wordt de uitdrukking y=ln(x) gebruikt. ‘ln’ staat voor logarithmus naturalis.

We hadden ontdekt dat we grootte-ordes van getallen kunnen optellen als equivalent om te vermenigvuldigen. Dat wordt met logaritmes als volgt uitgedrukt:

Het is een algemene uitdrukking van het voorbeeld dat we reeds aanhaalden:

OK. So far so good. Logaritmes zijn dus een ander woord voor grootte-orde, maar wanneer gaan we nu beginnen schuiven met de rekenlat? Wat gebeurt er eigenlijk wanneer we schuiven met een gewone lat? Zoals hieronder afgebeeld kan je door te schuiven met een normale lat een optelling uitvoeren. Hieronder zie een optelling 6+4, je legt de nul-waarde van de tweede lat bij zes, en bij het getal 4 kunnen we aflezen dat de som van 6+4 gelijk is aan tien.

20190228_215126.jpg

Nu komt de aap uit de mouw! In plaats van een gewone schaal op een lat nemen we een logaritmische schaal, waarbij gelijke afstanden overeenkomen met gelijke verhoudingen. Nu zal er waarschijnlijk ergens een belletje rinkelen of zelfs een halve beiaard want dat is ook hoe de frequenties achter de toetsen van de piano werken (Alle piano’s zijn een beetje vals) en ook hoe de versnellingen op een fiets werken (De derailleur dirigeert de dans van tandwielen en trapcadans). Je zou je a fortiori kunnen afvragen of er meer is in het leven dan logaritmes…

Hieronder, op een echte rekenlat, zie je dat alle getallen die zich verhouden met een zelfde factor even ver van mekaar staan. De getallen 2, 4 en 8 liggen op zelfde tussenafstand. Alsook de getallen 1, 3 en 9. Door op de ene lat 1 (dat is voor alle getallen grootte-orde 0) gelijk te leggen met een getal op de andere lat (hier 2), vind je voor alle getallen de vermenigvuldiging met 2. In het voorbeeld hieronder wordt 2 vermenigvuldigd met 3, en wonder boven wonder dat is 6!

sliderule

Een vermenigvuldiging:

wordt dus hocus pocus op een rekenlat een optelling:

Uiteraard kan je nog veel meer met een rekenlat, maar het basis-principe zijn de logaritmische schalen die er voor zorgen dat er zich bij elke schuifbeweging een vermenigvuldiging voltrekt. En zo hebben onze grootvaders zich uren over hun rekenlat gebogen om te rekenen, of dat hebben ze ons tenminste wijsgemaakt…

Googolplexian groeten,

T.E.

 

 

miss slide rule