Dobble. Zeggen dat je zenuwen gesloopt worden is misschien overdreven, maar je zenuwen worden toch serieus onder druk gezet. (Zoveel bouwkundige uitdrukkingen in ons dagelijks leven waar je op kunt bouwen!) Je hebt kaarten met daarop 8 verschillende symbolen en elke twee kaarten hebben slechts één gemeenschappelijk symbool. En dat moet je natuurlijk zo snel mogelijk in de mot hebben om te winnen. En kinderen kunnen er verduiveld goed in zijn. Maar wacht eens even… stel dat je meer of minder symbolen per kaart hebt… papa moet even iets gaan opzoeken, meisjes!

En ja… net wat ik dacht. Er bestaat een formule dat aangeeft wat het maximale aantal kaartjes is dat je kan maken met een bepaald aantal symbolen op je kaart. Voor een zeer eenvoudig geval van 2 symbolen per kaart kan je gemakkelijk uitzoeken dat het maximaal aantal kaarten 3 is. Stel dat de symbolen A, B en C zijn, dan zul je 3 kaartjes hebben: AB, AC en CB. Ieder kaartje heeft inderdaad slechts één gemeenschappelijk symbool. We kunnen dus al stellen dat 2 symbolen –> 3 kaartjes. Hieronder een grafiek waarop de kaartjes zijn weergegeven en de lijnen tonen aan welke symbool de kaarten gemeenschappelijk hebben.

De grafiek heeft de volgende eigenschappen (lijnen staan voor symbolen, kaarten zijn de snijpunten):

• Gelijk welke twee kaarten zijn telkens verbonden met één lijn (dat zorgt er voor dat er tussen elke twee kaarten een gemeenschappelijk symbool is)
• Gelijk welke twee lijnen snijden slechts in één kaart (zorgt ervoor dat er slechts één gemeenschappelijk symbool is)

So far so good, maar wat met 3 symbolen per kaart? Hoeveel verschillende symbolen en dus hoeveel kaarten kan je nu maken? Laten we maar direct proberen een grafiek te maken waar elke kaart het kruispunt is van 3 lijnen (3 symbolen per kaart)… In de grafiek staan 4 kaarten en we maken gebruik van 6 symbolen A tot F.

Maar we kunnen met 3 symbolen verder gaan dan 4 kaarten, hieronder een grafiek van het maximaal mogelijke aantal kaarten met 3 symbolen. Ook hier geldt dat alle twee kaarten verbonden zijn met een lijn, en dat 2 lijnen slechts op één punt snijden. En inderdaad, niemand zei dat het rechte lijnen moesten zijn hé. Vervang de letters door leuke tekeningen en je kan al een zeer eenvoudige Dobble-spel samenstellen van 7 kaarten met telkens 3 symbolen op de kaart.

Dus met 2 symbolen per kaart vinden we een maximum van 3 kaarten en 3 verschillende symbolen. En met 3 symbolen vinden we maximum 7 kaarten en 7 verschillende symbolen: ABC, CFG, CDE, BEG, AEF, BDF en ADG. Het spreekt misschien iets meer aan met echte symbolen en mooie kleurtjes:

Het kan wiskundig aangetoond worden dat als we r symbolen per kaart kiezen het totaal aantal kaarten N (en ook het totaal aantal verschillende symbolen) gelijk is aan:

Dit lijkt inderdaad te kloppen voor r=2, dan wordt N=3. Bij r=3 vinden we dat N gelijk is aan 7. Deze ‘Dobble’-formule blijft geldig voor hogere waarden van r. Maar het maken van de grafiek wordt dan steeds wat complexer. stel nu dat we r=4 nemen, dan krijgen we een totaal van N=13, een bijhorende grafiek vind je hieronder. De zwarte punten staan voor de 13 kaarten en de 4 lijnen die er snijden stellen de symbolen voor, hier voorgesteld als 13 verschillende kleuren.

En zo kunnen we verder gaan en voor r=5 vinden we N=21.

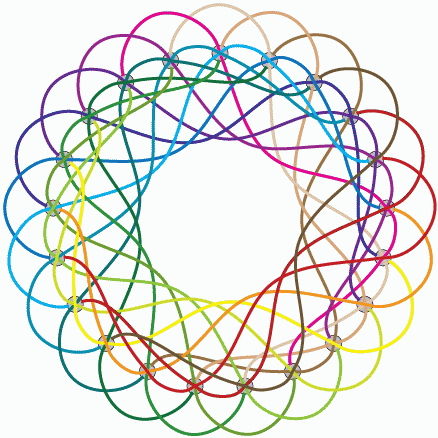
En voor 8 symbolen per kaart, zoals bij het Dobble-spel vinden we N=57. Ook hiervan heb ik een grafische weergave gevonden, je kan zien dat voor kaart 1 helemaal in het midden er 8 lijnen samenkomen.

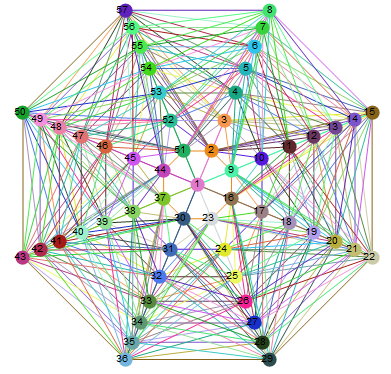
Maar wat merken we op als we de kaarten van Dobble tellen? Weliswaar 57 verschillende symbolen, maar slechts 55 kaarten! Dit wil zeggen dat er nog 2 unieke kaarten kunnen aangevuld worden aan het spelletje Dobble. Welke precies? Daar ben je ook al snel een avondje mee zoet denk ik.

Waarom 55 kaarten en niet 57? Dat is geen complot of vergetelheid denk ik, maar gewoon optimalisatie bij het drukken. Bij een gewoon spel speelkaarten stel je ook vast dat er naast de 52 kaarten (13×4) ook nog 2 jokers bijzitten en nog een instructie-kaart, wat het totaal brengt op 55 kaarten, die netjes in 11 rijen van 5 kaarten voorbij zoeven in de drukkerij… Ja, we eindigen gewoon met boerenverstand en de tafel van 5.

Tot zover een spelletje Dobble spelen met papa…

Aan iedereen unieke groeten,

T.E.