Wanneer er een belangrijke wielerwedstrijd is, zoals het WK, wil ik ook altijd met een zeker fietsgevoel voor de tv zitten en daarom ga ik in de voormiddag meestal een toertje doen. Omdat ik onlangs een beugel heb geïnstalleerd om m’n fiets omhoog te hangen (dat hoort zo in een georganiseerde garage), keek ik net voor ik m’n fiets van de haak haalde recht naar de derailleur: een knap staaltje techniek dat ervoor zorgt dat je in een comfortabele cadans kan rijden. Wind tegen, bergop, met de wind mee of bergaf. Altijd het juiste verzet.

Het woord derailleur is onlosmakelijk verbonden met de fiets, niemand zal zeggen dat hij miserie heeft met de derailleur van z’n auto. Het woord ‘derailleur’ klinkt ook net alsof je een ketting hoort rollen over tandjes. En als je het woord ‘derailleur’ laat vallen lijkt het direct of je een ervaren rot in het wielrennen bent. Het komt uit de tijd dat het Frans nog de lingua franca was in het fietswereldje, en als ik menig fietshersteller of de televisiecommentator hoor is dat nog steeds zo. Zo rem je met je ‘frein’ en als je op de borduur rijdt moet je opletten voor je ‘janten’. En ‘coureurs’ die ‘demarreren’ uit het peloton moeten opletten dat ze geen ‘chasse patate’ doen. Alhoewel, ik ben niet helemaal zeker of Voltaire deze uitdrukking frequenteerde.

‘Een tandje bijsteken’ is een wijdverbreide uitdrukking die gebruikt wordt wanneer er nog net dat ietsje inspanning meer nodig is of gevraagd wordt. Om dat tandje bij te steken heb je een derailleur nodig, en ironisch genoeg maak je het jezelf gemakkelijker wanneer je achteraan een tandje bijsteekt en het spreekwoord preciseert niet de ligging van het tandwiel. Dringend tijd om eens na te gaan hoe dat nu juist zit. De bedoeling is dat je met je pedalen een aangename trapfrequentie kan trappen, bv. 90 RPM (rounds per minute).

Het verzet is de afstand die je aflegt met één trapomwenteling, dus bergop en tegen wind hebben we een klein verzet nodig en wind achter of bergaf hebben we een groot verzet van doen. Wanneer we vooraan en achteraan evenveel tandwielen hebben dan is het verzet gelijk aan één wielomtrek. Bij een normale koersfiets is dat 2,1 m. Het aantal tandwielen voor en achter maakt niet uit, enkel de verhouding van beide. Daar voelen we inderdaad al een formule opkomen. Als we vooraan dubbel zoveel tandjes hebben als achteraan, dan zal het achterwiel 2 keer moeten draaien bij één predaalomwenteling. In dat geval is het verzet het dubbele van de wielomtrek, dus 4,2 m. Algemeen kan men dus stellen dat:

Ik heb zonet tandjes zitten tellen op de tandwielen van mijn koersfiets en mijn grootste verzet wordt bepaald door het grootste tandwiel voor (53) en het kleinste achter (12):

Als je dat verzet ronddraait met een trapfrequentie van 100 RPM dan heb je (in theorie) het werelduurrecord van sir Bradly Wiggins (54,526 km) gebroken, als je die snelheid tenminste één uur zou volhouden.

Wiggins reed trouwens z’n uurrecord met een versnelling 58/14. Verbazend, want dat is een kleiner verzet dan mijn grootste verzet: 58/14 is goed voor een verzet van 8,7 m. Hij zal dus met een trapfrequentie van ca. 105 RPM gereden hebben.

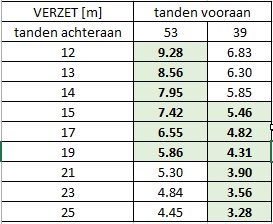
Maar er is meer! Want de derailleur zorgt er voor dat je voor en achter kan kiezen uit verschillende tandwielen. Vooraan heb ik twee tandwielen: het grootste heeft 53 tanden en het kleinste heeft er 39. Achteraan heb ik een tandwielcassette met maar liefst 9 tandwielen van groot naar klein: 25-23-21-19-17-15-14-13-12. Mijn kleinste verzet bedraagt dus 39/25 maal mijn wielomtrek wat neerkomt op 3,276m. De verhouding van het grootste en het kleinste verzet wordt het versnellingsbereik genoemd, hier is dit 2,83. Soms wordt dit in procent uitgedrukt: mijn koersfiets heeft een versnellingsbereik van 283% Om een echt groot versnellingsbereik te verwezenlijken heb je 3 tandwielen vooraan nodig,  dan kan je tot 600% gaan.

Ik heb 2×9=18 mogelijke combinaties, maar in realiteit heb ik maar 12 versnellingen omdat een combinatie 53/19 ongeveer hetzelfde verzet geeft als 39/14 zie ook onderstaande tabel, met in het groen de 12 effectieve versnellingen. Het leidt geen twijfel dat het verschil tussen combinaties en versnellingen al meermaals geleid heeft tot hoogoplopende caféruzies en misverstanden. In het genre van: ‘Wat zeg je? Ik heb geen 24 versnellingen? Kijk maar eens naar mijn fiets: 3 vooraan en 8 achteraan! Het kleinste kind kan dat toch zien?’. ‘Ja maar kijk eens naar uw verzet-tabel’. ‘Ik zal eens een verzet-tabel steken…’ Enzovoort, enzovoort…

Als we de verzetten van de 12 versnellingen uitzetten per versnelling dan zien we dat deze geen lineair verloop kennen. Dat is logisch want de verhoudingen tussen de opeenvolgende verzetten moet zo gelijk mogelijk zijn en niet de verschillen in verzet. Tiens, dat doet me denken aan de gelijke ratio tussen de frequenties van gelijke intervallen (zie: Alle piano’s zijn een beetje vals). De verhoudingen zijn hier geen verhoudingen van frequenties, maar verhoudingen van verzetten. De wiskunde achter beide fenomenen is krak hetzelfde.

We zoeken dus de gemiddelde ratio waarmee we 11 keer het kleinste verzet (3,276 m) kunnen vermenigvuldigen om uit te komen bij het grootste verzet (9,275):

Hieruit volgt:

Voor de lol zullen we dit eens uitrekenen met logaritmes (in dit geval met Briggse logaritmes met basis 10, maar dit mogen gerust ook Neperiaanse logaritmes zijn – voor iemand me beschuldigt van favoritisme)  zodat de machtsverheffing een vermenigvuldiging wordt, daarvoor gaan we linker- en rechterlid naar het parallelle universum van de logaritmes sturen:

Hieruit volgt:

En dus is de gemiddelde ratio:

Gemiddeld zal dus iedere versnelling een verzet hebben dat 10% hoger ligt dan de vorige versnelling. Maar het aantal tanden zijn discrete waarden, dus moet er een combinatie gezocht worden die zo dicht mogelijk bij de gemiddelde ratio ligt. Hieronder zijn de verzetten uitgezet ten opzichte van de verzetten bij gelijke ratio. Je kan duidelijk zien dat de ontwerper van mijn versnellingen zijn best gedaan heeft om zo dicht mogelijk aan te sluiten bij de curve van gelijke ratio’s, zodat iedere versnelling aanvoelt als een even zware relatieve verhoging van het verzet. Wat me ook weer doet denken aan de exponentiële constante groei uit: Dromen over het getal e, want we verkrijgen ook hier een exponentiële curve, zie ook onderstaande grafiek.

Maar als je het uurrecord wil breken, mag je dit allemaal vergeten, want dan hoef je maar één verzet te voorzien… En trappen maar!

Je zal al snel merken dat Wiggins een ongelofelijke prestatie heeft neergezet… ik probeer alvast bij een volgend fietstochtje eens één minuut de uurrecordsnelheid van Wiggins aan te houden. Ik kan het alleszins al niet meer steken op mijn verzet…

Ik heb door deze vernieuwde inzichten in de werking van mijn derailleur warempel zin gekregen om als de wiedeweerga mij stalen ros te bestijgen!

Sportieve groeten,

T.E.