Alle piano’s zijn een beetje vals

Vals is misschien een beetje kort door de bocht, maar toch is er het nodige kunst- en vliegwerk nodig geweest om de natuurlijke, ook wel reine, intervallen in het zwart-witte stramien van een piano samen te proppen. Met 7 witte toetsen en 5 zwarte toetsen heb je per toonladder 12 halve tonen op een piano. Dat kunst- en vliegwerk wordt ook wel een gelijkzwevende stemming genoemd.

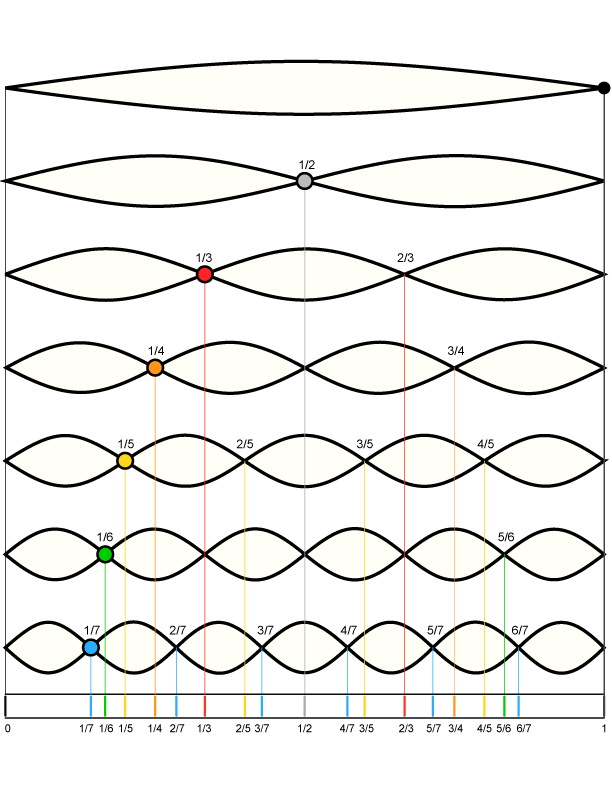
Mooie, reine intervallen hoor je in de boventonen van een snaar. Als je een snaar aanslaat dan hoor je niet alleen de grondfrequentie (een golf over de gehele snaarlengte), maar ook de boventonen. Dat zijn tonen waarbij er een gelijk aantal golfjes gemaakt worden over de snaarlengte, deze golfjes hebben een kleinere golflengte en klinken hoger dan de grondfrequentie. Je kan de snaar indelen in 2, 3, 4, 5 enzovoort golfjes die telkens een hogere boventoon zullen genereren, waarvan de frequentie 2, 3, 4, 5,… keer de frequentie van de grondtoon is. Dat zorgt ervoor dat verhoudingen tussen boventonen eenvoudige verhoudingen zullen hebben. Een verhouding $\frac{2}{1}$ is een octaaf en een verhouding $\frac{3}{2}$ is een reine kwint. Deze intervallen ervaren wij als een streling voor het oor…

harmonics2

Octaaf? Kwint? Wat moeten we ons daar nu bij voorstellen? Sluit je ogen en laat Judy Garland ‘Somewhere over the rainbow’ zingen in je hoofd. ‘Some-where’ is een octaaf, dat klinkt zo mooi samen dat we noten die een octaaf van elkaar zitten dezelfde naam geven bv. de lage do en de hoge do. Als je het probeert na te zingen kom je erachter dat een octaaf een serieuze stap is, maar als het lukt klinken de tonen heel natuurlijk bij elkaar. Dat is perfect wetenschappelijk verantwoord want de frequenties verhouden zich als 2 en 1. Verdubbelen we de frequentie dan komen we telkens een octaaf hoger uit. Dat is alleszins al handig om onze piano te stemmen!

Sluit nu opnieuw je ogen en zing luidkeels ‘Altijd is Kortjakje ziek’. Stop! Je hebt een kwint gezongen. ‘Altijd’ en ‘is’ vormen een reine kwint. Hier is de verhouding van de frequenties 3 op 2. Zingen we ‘altijd’ op pakwek 200 Hz (dat zijn het aantal trillingen per seconde) dan moeten we ‘is’ zingen op $\frac{3}{2}$ van 200 dus 300 Hz. Zonder deze kennis lukt het je uiteraard ook wel om Kortjakje te zingen. Als we perfect Kortjakje op een piano willen spelen willen we ook deze mooie verhouding horen!

Een andere verhouding is de kwart (4 op 3) en die zing je telkens wanneer je op een gezellige kerstavond ‘We wish you a happy christmas’ zingt. Tussen ‘We’ en ‘wish’ zit er een reine kwart. Zingen we ‘We’ op 300 Hz dan moet ‘wish’ op 400 Hz klinken. Netjes volgens de mooie frequentieverhoudingen, het zou leuk zijn moest dat ook lukken op de piano…

En wat nog mooier is: wanneer we eerst een kwint nemen $\frac{3}{2}$ en daarna een kwart $\frac{4}{3}$ dan komen we uit op $\frac{3}{2}\frac{4}{3}=\frac{4}{2}=2$ , netjes een octaaf. Wat gaan muziek en wiskundige verhoudingen mooi hand in hand!

En zo gaat het verder en passeren ook de grote terts (verhouding $\frac{5}{4}$ ) en de kleine terts (verhouding $\frac{6}{5}$ ) en nog een rits andere intervallen de revue. Met telkens mooie verhoudingen van frequenties en verwennerij voor onze oren. De halve toon komt overeen met een kleine secunde, een verhouding van $\frac{16}{15}$ .

Maar lang genoeg gezeten op onze roze wolk. Want op de piano zijn er 7 witte en 5 zwarte toetsen in een octaaf (12 halve tonen: do do# re mi-b mi fa fa# sol sol# la si-b si en terug do) Om 12 gelijke stappen te zetten zoeken we een verhouding die we 12 keer na elkaar kunnen vermenigvuldigen om dan precies op 2 uit te komen. Geen probleem, de wiskunde schiet ons te hulp: we zoeken verhouding x waarbij $x^{12}=2$ hieruit volgt dat $x=\sqrt[12]{2}$ . De gevonden factor is bijgevolg $\sqrt[12]{2}=1,05946....$ Met deze factor kunnen we gelijk welke frequentie 12 keer vermenigvuldigen om uit te komen op de dubbele frequentie en dat is precies één octaaf.

Trouwens er zijn nog wel natuurlijke fenomenen waarvan de ervaring van gelijke stappen (de ervaring van toonhoogte) in feite een exponentieel verloop heeft van de fysische grootheden, zoals de frequentie in dit geval. Het meten van pH (scheikunde) en decibel (geluidsterkte) zitten ook in hetzelfde schuifje. Van schuifje gesproken, ook de rekenlat (de voorloper van de rekenmachine) maakt gebruik van eigenschappen van de exponentiële functie en vooral van z’n inverse functie: de logaritmische functie! Het hoeft geen betoog dat dit ons te ver laat afdwalen… terug naar de piano!

Op de piano is een kwint 7 halve tonen, dus we berekenen $\sqrt[12]{2^{7}}=1,4983...$ wat een benadering is van $\frac{2}{3}=1,5$ maar dus toch niet netjes de verhouding is van een kwint. Zelfde verhaal bij de kwart (5 toetsen op de piano): $\sqrt[12]{2^{5}}=1,3348...$ een benadering van $\frac{4}{3}=1,3333...$ maar niet exact. En ook bij de andere intervallen loopt het een beetje (en soms behoorlijk veel) mis:

wat met de halve toon of de kleine secunde, met de natuurlijke frequentie verhouding $\frac{16}{15}=1,0666...$ ? Tja dat loopt ook mis want op een piano is de verhouding $\sqrt[12]{2}=1,05946....$ . Het komt nooit goed want rationale getallen (breuken) kunnen nooit gelijk zijn aan irrationele getallen $\sqrt[12]{2^{n}}$ Meer algemeen bestaan er geen natuurlijke getallen a, b en n waarbij $\left (\frac{a}{b} \right )^{n}=2$ . Daarom klinkt elke piano altijd een klein beetje vals zelfs al zouden we het octaaf in nog kleinere stukjes hakken (zo’n piano’s bestaan trouwens)… maar het klinkt wel mooier (en harmonischer) om te zeggen dat de piano gestemd is volgens een ‘gelijkzwevende stemming’.