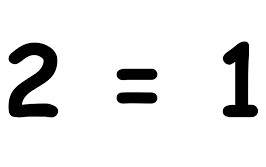Om te rekenen hebben we tegenwoordig rekenmachines en smartphones ter beschikking, maar er is een tijd geweest, nog niet eens zo lang geleden, dat alle bewerkingen met getallen manueel moesten gebeuren. Met pen, papier en veel monnikengeduld geraak je wel ergens, maar in grootvaders tijd hadden ze als hulpmiddel een rekenlat. Ik vroeg me al lang af hoe zo’n ding werkt, en ik heb me er één aangeschaft, ter ontsluiering van z’n geheimen.

Iedereen heeft wel eens twee kinderen horen bekvechten, waarbij de ene beweert wel duizend knikkers te hebben en waarbij de andere met hoongelach de andere duidelijk maakt dat hij er nog veel meer heeft: wel honderd! Waarbij knikkers inwisselbaar zijn in om het even wat, naargelang het onderwerp van de discussie. Het door elkaar haspelen van grootte-ordes is nu eenmaal hilarisch. Reeds in de lagere school leren we hoeveel nulletjes we moeten bijvoegen om een getal te vermenigvuldigen met honderd of duizend. Mijn dochter geeft me zonder verpinken de antwoorden: om met tien, honderd of duizend te vermenigvuldigen moet je respectievelijk één, twee en drie nulletjes toevoegen aan het getal. Zeer interessant want het vermenigvuldigen met veelvouden van 10 is dus in feite equivalent aan het optellen van nulletjes. We hebben dus van een vermenigvuldiging een optelling gemaakt…

Ik ben me er ter dege van bewust dat het optellen van nulletjes om tienduizend met pakweg een miljoen te vermenigvuldigen niet echt rocket science is, maar de dualiteit tussen optellen en vermenigvuldigen is het principe dat aan de basis ligt van de werking van een rekenlat. Er moet enkel nog een abstractiesausje over en het geheel moet nog wat gekruid worden met een ‘moeilijk woord’, maar het concept zal blijven dat we grootte-ordes van getallen optellen om ze te vermenigvuldigen. De bekvechtende kinderen van daarnet hadden het over grootte-ordes van tien. Honderd. Duizend. Miljoen. Miljard. En ga maar door… Het is duidelijk dat tien een centrale rol speelt in dit geval. De grootte orde van tienduizend is 4 en de grootte orde van een miljoen is 6. Het vermenigvuldigen van tienduizend en een miljoen is dus equivalent aan het optellen van de grootte ordes: 4+6=10.

Het abstractiesausje zullen we opdienen in twee gangen samen met twee vragen. De eerste vraag is: heeft elk getal een grootte orde? Affirmatief! Zoals je 10 kunt verheffen tot de 2de macht om 100 te bekomen, kan je perfect 10 verheffen tot de macht 2,5. Verheffen betekent letterlijk ‘naar een hoger niveau brengen’. Het antwoord op 10 tot de macht 2,5 is trouwens 316,227766… Het gaat alleszins serieus hard als we beginnen met verheffen, 10 tot de macht 80 is een schatting van het totaal aantal atomen in het heelal. We kunnen dus redelijk wat omspannen met 80 grootte-ordes van 10. Het aantal atomen in een mol: grootte-orde 23 (zie ook het stukje: Over een lepeltje, oceanen en moleculen). ‘Googol’ is de aanduiding voor de 100ste macht van 10, daar komt trouwens de naam Google vandaan.

Een ‘googolplex’ is 10 tot de macht googol, en we blijven ons wiskundehartje verheffen want een ‘googolplexian’ is dan weer 10 tot de macht googolplex. Letterlijk niet te bevatten want er zijn niet genoeg atomen in het heelal om te voorzien in alle nullen en ik kan dan ook met recht en rede zeggen dat dit ons veel te ver leidt. Als je nog harder wil gaan dan het machtsverheffen, moet je zeker eens zoeken (Googelen bijvoorbeeld) naar het ‘getal van Graham’.

De tweede vraag is: kan een ander getal dan 10 gebruikt worden als het grondtal voor de grootte-orde? En ook hier is het antwoord eveneens positief. Natuurlijk kan je dat. Het binair talstelsel is een mooi voorbeeld, waarbij het grondtal 2 is. (zie ook: Schaakmat voor koning Shirham) Maar waarom het gemakkelijk maken als het ook moeilijk kan? Waarom nemen we niet gewoon het grondtal e? (zie ook: Dromen over het getal e) Hiermee kunnen we zeer goed continue groei wiskundig omschrijven. En in de natuur zijn er nogal wat zaken die volgens dat principe werken, ik denk maar aan de afname van radioactiviteit. Als we e nemen als grondtal dan zal de x-de macht van e de continue 100%-groei weergeven in een tijdspanne x. Maar zoals we alle getallen kunnen uitdrukken als machten van 10 of 2, kunnen we evengoed alle getallen uitdrukken als een macht van e. Uiteraard mag dit niemand ervan weerhouden om nog een ander grondtal te nemen, gewoon om tegen tjok te zijn. (zie ook: De ontplooiing van het verhaal van ‘tegen tjok’ rolmodel Britney Gallivan).

Na deze flexibiliteit naar grootte-orde en naar grondtal, is het dringend tijd voor het kruiden van het geheel met een moeilijk woorden. We hebben steeds gesproken over de grootte-orde van een getal op basis van een grondtal. Zo is de grootte-orde van 1000 op basis van grondtal 10 gelijk aan 3. En is de grootte-orde van 16 op basis van grondtal 2 gelijk aan 4. Vanaf nu gaan we grootte-orde vervangen door ‘logaritme’. Laten we nu bovenstaande voorbeelden nemen dan zeggen we dat de logaritme met grondtal 10 van 1000 gelijk is aan 3. Notatie:

en de logaritme met grondtal 2 van 16 gelijk is aan 4. Notatie:

Meer algemeen geldt de volgende definitie:

Wanneer we als grondtal e nemen, wordt de uitdrukking y=ln(x) gebruikt. ‘ln’ staat voor logarithmus naturalis.

We hadden ontdekt dat we grootte-ordes van getallen kunnen optellen als equivalent om te vermenigvuldigen. Dat wordt met logaritmes als volgt uitgedrukt:

Het is een algemene uitdrukking van het voorbeeld dat we reeds aanhaalden:

OK. So far so good. Logaritmes zijn dus een ander woord voor grootte-orde, maar wanneer gaan we nu beginnen schuiven met de rekenlat? Wat gebeurt er eigenlijk wanneer we schuiven met een gewone lat? Zoals hieronder afgebeeld kan je door te schuiven met een normale lat een optelling uitvoeren. Hieronder zie een optelling 6+4, je legt de nul-waarde van de tweede lat bij zes, en bij het getal 4 kunnen we aflezen dat de som van 6+4 gelijk is aan tien.

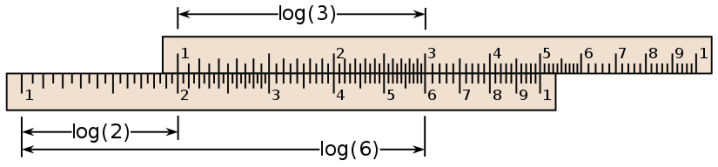
Nu komt de aap uit de mouw! In plaats van een gewone schaal op een lat nemen we een logaritmische schaal, waarbij gelijke afstanden overeenkomen met gelijke verhoudingen. Nu zal er waarschijnlijk ergens een belletje rinkelen of zelfs een halve beiaard want dat is ook hoe de frequenties achter de toetsen van de piano werken (Alle piano’s zijn een beetje vals) en ook hoe de versnellingen op een fiets werken (De derailleur dirigeert de dans van tandwielen en trapcadans). Je zou je a fortiori kunnen afvragen of er meer is in het leven dan logaritmes…

Hieronder, op een echte rekenlat, zie je dat alle getallen die zich verhouden met een zelfde factor even ver van mekaar staan. De getallen 2, 4 en 8 liggen op zelfde tussenafstand. Alsook de getallen 1, 3 en 9. Door op de ene lat 1 (dat is voor alle getallen grootte-orde 0) gelijk te leggen met een getal op de andere lat (hier 2), vind je voor alle getallen de vermenigvuldiging met 2. In het voorbeeld hieronder wordt 2 vermenigvuldigd met 3, en wonder boven wonder dat is 6!

Een vermenigvuldiging:

wordt dus hocus pocus op een rekenlat een optelling:

Uiteraard kan je nog veel meer met een rekenlat, maar het basis-principe zijn de logaritmische schalen die er voor zorgen dat er zich bij elke schuifbeweging een vermenigvuldiging voltrekt. En zo hebben onze grootvaders zich uren over hun rekenlat gebogen om te rekenen, of dat hebben ze ons tenminste wijsgemaakt…

Googolplexian groeten,

T.E.