Er wordt niet enkel in wetenschappelijke kringen over spanning gesproken. Spanningen kunnen hoog oplopen tussen mensen of landen. Een boek kan spannend zijn. Ons dagelijks leven zit uiteraard ook vol stress (of spanning). We geven aan dat het een toestand is die in extremis kan leiden tot ruzie, oorlog, ontknoping of een zenuwinzinking… Een zwaar belastende job geeft je veel stress. De analogie voor materialen is zeer gelijklopend: een zwaar belast materiaal zal onder hoge spanning staan, totdat de spanning te hoog oploopt en het materiaal bezwijkt.

Als voorproefje voor dit schrijven had ik verkondigd dat krachten niet bestaan in realiteit (Over structuren en de derde wet van Newton), dat zal ik hier zeker niet ontkrachten, wel toelichten. Krachten bestaan niet in de zin dat een krachtvector een wiskundige constructie is zoals een rechte of een lijnstuk en daardoor geen breedte heeft en daarmee moeilijk verzoenbaar is met de werkelijkheid die zich in alle ruimtelijkheid voor ons ontplooit. In deze werkelijkheid is de spanning die optreedt in materialen een veel betere maatstaf van de toestand van een materiaal dan kracht. Bouwkundigen zullen daarom aan het einde van het verhaal vooral geïnteresseerd zijn in de spanningen die heersen in de materialen waarin constructies zijn opgebouwd, deze spanningen worden gedefinieerd als de kracht per oppervlakte:

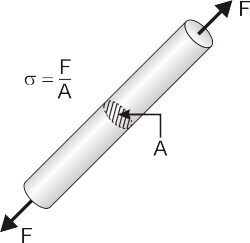
De Griekse kleine letter sigma wordt in de sterkteleer meestal als symbool gebruikt voor spanning en deze wordt uitgedrukt in Newton per vierkante meter (N/m²), algemene spanningen in de natuurkunde worden veelal uitgedrukt met het symbool p (pressure). De eenheid van spanning is pascal (Pa) waarbij 1 Pa = 1 N/ m². Deze eenheden maken deel uit van de uniforme internationale standaardeenheden (het SI-stelsel), en het pleit zeer voor de wereldwijde samenwerking van wetenschappers dat bijna alle landen diezelfde eenheden gebruiken. Het zou werkelijk onhandig zijn als bepaalde landen spanning in pakweg pond per vierkante duim zouden uitdrukken. Het is dan in het licht van de uniformisering betreurenswaardig dat we nota bene de Verenigde Staten van Amerika terug vinden in het rijtje van landen, naast Myanmar en Liberia, die niet officieel het SI-stelsel hebben ingevoerd. Dat maakt overigens dat bouwkundige naslagwerken (en ik vermoed bij uitbreiding veel wetenschappelijke boeken) uit de VS quasi waardeloos zijn in de rest van de wereld en de ontgoocheling is dan ook groot wanneer een aangekocht boek in deze middeleeuwse eenheden blijkt opgesteld te zijn. Voor degenen die toch de omrekening willen doen: 1 psi = ca. 6895 Pa, waarbij psi staat voor ‘pounds per square inch’.

Maar laten wij ons niet al te zeer verkneukelen in deze trans-Atlantische bizariteit. Wanneer wij spreken over een bloeddruk die 14 over 7 is dan spreken wij ook helemaal niet in pascal of N/m², maar hebben we het over kwikdruk in cmHg. Het was gebruikelijk om de luchtdruk te meten met behulp van een kolom kwik, de normale atmosferische luchtdruk bedraagt zo’n 760 mmHg. Kwik is veel zwaarder dan andere vloeistoffen, en daarom handiger qua formaat, zo is het historisch gegroeid dat mmHg de eenheid voor bloeddruk is geworden en 1 mmHg is trouwens gelijk aan ca. 133,322 Pa. De schaal is nu zo ingeburgerd dat het standaard is om lichaamsvloeistoffen uit te drukken in mmHg, voor alle andere toepassingen is het SI-stelsel de standaard. Een normale bloeddruk van 120 mmHg komt overeen met een druk van 16 kPa.

Het feit dat de luchtdruk op aarde schommelt rond 100 kPa (komt overeen met 1 bar) is op het eerste zicht verwonderlijk. Op ieder van ons heerst er een druk die equivalent is met een waterkolom van 10 m. Dat is een behoorlijke druk en zoals veel zaken die niet opvallen, valt hij pas op wanneer we hem moeten missen. Zoals op de maan, waar zonder ruimtepak onze lichaamssappen zouden koken, bij het ontbreken van voldoende luchtdruk, wat steeds tot een gewisse dood zou leiden. Dat doet me denken aan de koningin van de nacht uit De Toverfluit die zingt: “Der Hölle Rache kocht in Meinem Herzen”. Het bloed kookt in haar hart! Extreme drukken vinden we in het heelal: zowel het bijna absolute vacuüm in de verste leegtes van ons universum als de werkelijk extreme drukken binnen in een neutronenster. Daar heersen zo’n extreme drukken dat het onbegonnen is om ook maar enige vergelijking te maken. Toch een poging: een theelepeltje neutronenster weegt 10 miljoen ton, of evenveel als 50 keer het gewicht van de grootste containerschepen die er bestaan…

Maar terug naar spanningen in materialen, deze zijn nog een paar grootte ordes groter dan de luchtdruk en worden meestal uitgedrukt in MPa (één miljoen Pa). De maximale trekspanning in een materiaal wordt de treksterkte genoemd. Zo is de treksterkte van normaal staal 420 MPa. Hout is tien keer minder sterk: de sterkte van dennenhout is 40 MPa. Een enorm sterk materiaal is een koolstof nanobuis met een sterkte van maar liefst 62.000 MPa. En de treksterkte van beton sluit vele lijstjes van materialen af met een bedroevende 2 MPa.

Hoe is het mogelijk dat we zoveel gebouwen hebben opgetrokken met zo’n zwak materiaal als beton? Om dit te verklaren moeten we begrijpen dat spanningen zich manifesteren in twee verschijningsvormen: drukspanningen en trekspanningen. De luchtdruk is ontegensprekelijk een drukspanning, maar de treksterkte van materialen gaat over de trekspanningen. Beton heeft weliswaar een lage treksterkte, maar kan zeker z’n mannetje staan als het over druksterkte gaat. Dat is trouwens z’n sterkste punt, sterkteklassen van beton verwijzen altijd naar de druksterkte. Zo is C30/37 een beton met een karakteristieke druksterkte van 30 MPa op een proefcilinder (de 37 MPa slaat op de druksterkte op een proefkubus). Gewapend beton is een mooi huwelijk tussen beton en staal waarbij beton de drukspanningen voor z’n rekening neemt het staal de trekspanningen. Het gezegende aan dit huwelijk is dat beide materialen op dezelfde manier reageren op temperatuurschommelingen en dat beton het staal beschermd tegen corrosie.

Dat spanningen een ander fenomeen zijn dan krachten kan je zelf ervaren als je een scherp potlood tussen duim en wijsvinger houdt en die samendrukt. De kracht in het potlood is uiteraard dezelfde, maar bij de kleine oppervlakte van de punt zal de spanning groter zijn (kracht gedeeld door kleiner oppervlak) en dat zie je ook afgetekend in je huid. Het is een welbekend voorbeeld dat een olifant gemakkelijker door het zand stapt dan iemand op stiletto’s. Dat heeft niets te maken met de kracht, maar alles met de spanning, want de spanning op de grond van de stiletto’s is veel groter dan de spanning veroorzaakt door een olifantenpoot. Laat ons dat eens snel berekenen voor een dame van 60 kg met hakken van diameter 1 cm diameter en een olifant van 5 ton met 4 poten met een diameter van 30 cm.

De druk onder een stiletto is wel 20 keer hoger dan de druk onder een olifantenpoot, daarmee loopt de olifant beduidend vlotter door het zand dan de dame in kwestie en begrijpt iedereen beduidend beter het verschil tussen krachten en spanningen.

Van de olifantenpoot naar een stevige kolom in een gebouw is maar een kleine stap het zijn allebei elementen waar er drukspanningen in heersen. Een mooi voorbeeld van trekspanningen zijn de spanningen in een kabel, en bij uitbreiding alle constructies die gebruik maken van kabels. Hangbruggen en tuibruggen zijn pareltjes van voorbeelden.

Spanning. Het doet wat met een mens. Maar wat doet spanning met materialen? Vroeg of laat komt het tot breuk en sterke materialen zijn bestand tegen grote spanningen, maar hoe reageert een materiaal op spanning? We hadden het vorige keer over Newton en z’n wet over actie en reactie die aan de basis licht van de krachtenanalyse van een structuur. Maar minstens even belangrijk voor de bouwkundige analyse van structuren is de wet van z’n tijdsgenoot en rivaal: Robert Hooke. De wet van Hooke is werkelijk de Alfa en de Omega van de sterkteleer.

In een volgend schrijven zal de wet van Hooke onder de loep genomen worden, waarmee dit schrijven eindigt in spanning!

Spannende groeten,

T.E.