“Ik heb nog iets waar je over kan schrijven! Als ik deze emmer draai, waarom is het water dan lager in het midden en hoger aan de randen?” Met deze vraag gaf mijn oudste dochter me een aanzet voor dit stukje. Het draaien zorgt inderdaad voor een afbuiging van het wateroppervlak, welk soort oppervlak zou dit zijn? En welke mysterieuze krachten zorgen voor dit gebogen wateroppervlak?

Moest het wateroppervlakte werkelijk perfect horizontaal zijn, dan zouden we leven op een platte schijf. De wetenschappelijke consensus is echter dat de aarde waar wij op aanmodderen min of meer een bol is, ondanks de verbeten pogingen van organisaties als The Flat Earth Society, om ons te overtuigen van het tegendeel. Deze complottheorie woekert als een taaie distel tussen de andere complottheorieën. Het bewijst des te meer dat de wetenschappelijke methode niet ingebakken zit in onze intuïtie en dat niet iedereen ertoe komt om wetenschappelijke argumenten naar waarde te schatten, zichtzelf te overtuigen en desnoods van mening te veranderen. Ook religies tonen aan dat de mens zich perfect spiritueel en moreel kan laven aan materie die niet noodzakelijk de uitkomst is van een wetenschappelijk onderbouwd model. De evolutie heeft ons gezegend met het instrument intelligentie, maar we zijn allerminst gezegend met een queeste naar waarheid.

Oeps, dat ging even heel snel van een emmer water naar evolutietheorie… Terug bij de les! Een lokaal systeem van een emmer water ligt op zo’n grote afstand van het zwaartepunt van de aarde dat het oppervlak van stilstaand water als horizontaal mag beschouwd worden. Op elk punt ter wereld geldt dat de inwerkende kracht van de zwaartekracht loodrecht staat op het wateroppervlak, gericht naar het zwaartepunt van de aardbol.

Ik verbaasde me vroeger over de bolvorm van zon, sterren en planeten, maar nu besef ik dat het simpelweg een doorslagje is van de werking van de zwaartekracht. Zoals een waterdruppel in gewichtloze toestand bolvormig is, zo zijn ook de planeten bolvormig. En het wateroppervlak van de aarde is in feite een toestand van gelijke potentiële energie. Zoals we bij het vullen van een emmer niet verwonderd zijn over het horizontale wateroppervlak, hoeven we ook niet verwonderd te zijn dat samenklonterende vloeibare massa in het heelal bolvormig wordt.

Door het draaien wordt de watermassa in een roterende beweging gebracht. En dan komen de woorden ‘middelpuntvliegende’ of ‘middelpuntvliedende’ kracht al gauw op het puntje van onze tong liggen. Maar verrassend genoeg bestaat deze kracht niet echt (dit lijkt wel de start van een complottheorie). Deze kracht lijkt te bestaan, maar in feite gehoorzaamt het fenomeen volgzaam de wetten van Newton. Laat ik als voorbeeld hamerslingeren of kogelslingeren nemen, een leuke sport die ook in anderhalvemeter-tijd probleemloos kan beoefend worden. De eerste wet van Newton stelt dat bij het ontbreken van inwerkende kracht het voorwerp in rechte lijn wil voortbewegen. Dat gebeurt wanneer de atleet het kleinood loslaat. Zonder aardse zwaartekracht en luchtwrijving zou de kogel eeuwig in rechte lijn op de zelfde snelheid door het heelal blijven klieven. Om de kogel voldoende basissnelheid te geven wordt de kogel zo snel mogelijk rondgeslingerd, de kracht in de ketting, die we vroeger de middelpuntvliedende kracht zouden genoemd hebben is in feite de kracht nodig om de kogel te laten afbuigen van z’n rechte lijn, een bocht is immers een versnelling haaks op de richting van de beweging. Dit komt regelrecht uit de tweede wet van Newton: puur een verhaal van inertie, dus. De kracht nodig om een massa m op een cirkelvormige baan met straal r met constante hoeksnelheid ω te houden is:

Uit de bocht vliegen is het verlies aan weerstand om deze inertiekracht tegen te gaan. Bij auto’s wordt deze weerstand veroorzaakt door de wrijvingsweerstand van de wielen op het wegdek. De snelheid v van een voertuig in een bocht is gelijk aan de hoeksnelheid ω vermenigvuldigd met de straal r. De inertiekracht wordt herschreven in functie van de snelheid:

De bovenstaande formule leert ons dat er 3 oorzaken kunnen zijn om uit de bocht te vliegen. Ten eerste: het verhogen van de massa. Een zware vrachtwagen zal sneller uit de bocht vliegen dan een licht exemplaar. Ten tweede: het toenemen van de snelheid. Hoe sneller je een bocht wil nemen hoe groter de kans op ontsporing, dit effect weegt door want het is een kwadratisch verband. En ten slotte: de straal van de bocht. Hoe kleiner de straal van de bocht hoe groter de kracht. Daarom kan je probleemloos een bocht van een klaverbladknooppunt aan 70 km/u nemen en is het bijna onmogelijk om een klein rond puntje te nemen aan 70 km/u, tenzij je er recht over vlamt.

Wanneer we een waterdruppel beschouwen op het afgebogen wateroppervlak van een roterende emmer dan werkt zowel de horizontale inertiekracht als de zwaartekracht mg in op de beschouwde druppel. Aangezien het wateroppervlak loodrecht staat op de resulterende kracht is de helling dy/dx van het wateroppervlak evenredig is met de afstand x tot aan de rotatie as.

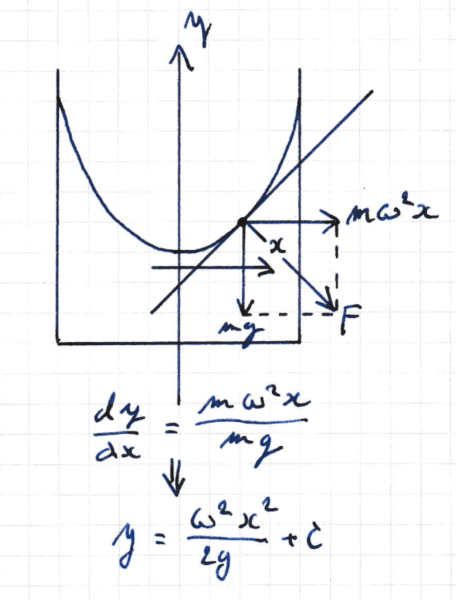
Een wateroppervlak zoeken waarvan de helling in ieder punt is geweten, is wiskundig vertaald een afgeleide functie integreren om de basisfunctie te vinden, hierbij is nog een constante C te bepalen. Dat is normaal want de helling van het wateroppervlak is onafhankelijk van het initiële waterniveau in de emmer, maar het wateroppervlak zelf is dat natuurlijk allerminst. Het besluit is dat het wateroppervlak in de emmer een omwentelingsparaboloïde is.

Meer algemeen zullen horizontale krachten op een watermassa tot gevolg hebben dat het wateroppervlak gebogen wordt. Probeer maar eens een kopje koffie recht te houden in een stevig optrekkende wagen en denk maar aan machtige stormwinden op zee die het wateroppervlak meters hoog de lucht injagen. Maar ook minder spectaculaire pogingen eindigen vaak in gemors. Het wandelen met een kopje koffie van de koffiemachine tot aan je bureau is een proces waarbij het gemiddelde staptempo jammer genoeg flirt met één van de eigenfrequenties van het systeem van een gevuld kopje koffie. Dit betekent dat ook bij het in acht houden van een zekere hoeveelheid voorzichtigheid het systeem toch zeer snel zal leiden tot extreme pieken van vloeistofhoogte. Het initiële niveau laag houden is een slim idee. Andere minder spectaculaire voorzorgsmaatregelen die volgen uit het wetenschappelijk onderzoek zijn niet te snel bewegen en goed kijken naar je koffie… daar hadden we misschien ook zelf kunnen opkomen.

De enige optie om af te rekenen met klotsende toestanden is het wegnemen van de horizontale kracht. Dit kan door het systeem bovenaan van een scharnier te voorzien. Als we een emmer aan een touw hangen en de emmer nergens tegen laten botsen dan zullen er zich geen horizontale krachten kunnen aangrijpen aan de watermassa. Het scharnier bovenaan is een onderdeel van het systeem dat niet toelaat dat er andere krachten in het systeem kunnen ontstaan dan de trekkracht in het touw, en deze kracht is steeds loodrecht op de emmer. Elke horizontale kracht die inwerkt op het systeem ter hoogte van het scharnier wordt gecompenseerd door de hoek die het systeem inneemt ten opzichte van het scharnier. Doordat er zich op deze manier geen horizontale krachten kunnen ontwikkelen in de watermassa loodrecht op de aslijn van het recipiënt naar het draagscharnier is morsen (quasi) onmogelijk geworden.

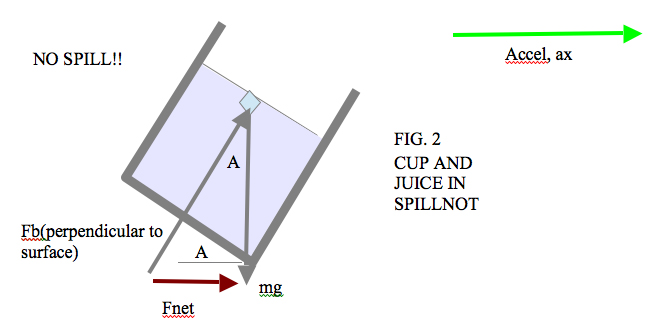
Een Spillnot is gebruiksvoorwerp gebaseerd op deze wetenschap. Je zet een kopje koffie op de Spillnot en je draagt alles met het touwtje bovenaan dat dienst doet als scharnier, waardoor er geen horizontale versnellingen ontstaan ter hoogte van het kopje, en bijgevolg geen gemors! Beetje reclame voor zo’n leuk gadget kan geen kwaad hé. Perfect educatief verantwoord en je kan hem altijd komen testen.

Grote geuten gemorste groeten,

T.E.