Het lijkt een goede ingeving: waarom kunnen we niet gewoon iedereen op Corona testen? Het antwoord is redelijk simpel: er zouden teveel mensen onterecht positief testen. Onterecht? Jazeker: er is immers altijd een kans dat de uitslag van een test verkeerd is, want de test is niet onfeilbaar. Daarom is het enkel relevant om de ‘verdachte’ gevallen uit een risico-groep te testen. En dat kan ook gemakkelijk wiskundig verklaard worden.

We gaan eerst enkele begrippen toelichten die de accuraatheid van een medische test uitdrukken:

• De sensitiviteit is de kans op een terecht positieve uitslag. Een positieve uitslag, bij het gegeven dat je besmet bent. Deze kans wordt genoteerd als: P(POS|Covid). Bij de meeste Covid testen ligt dit op ongeveer 71%. Dat is een vrij lage waarde. Dat betekent dat er 30% mensen zijn waarbij de besmetting niet wordt opgemerkt door de test. De zogenoemde vals negatieven.
• De specificiteit is de kans op een terechte negatieve uitslag. Een negatieve uitslag, gegeven dat je niet besmet bent, wordt genoteerd als: P(NEG|nietCovid). De specificiteit van de huidige Covid-testen is nog onduidelijk. We kunnen hier optimistisch in zijn en er van uit gaan dat deze 99% bedraagt. Dat wil zeggen dat 1% van de mensen die niet besmet zijn, toch een positief zal testen. Dan zijn dan de vals positieven.
• De prevalentie is de kans op besmetting voor een bepaalde populatie, op een bepaald moment. Hierbij dient opgemerkte te worden dat een populatie een totale populatie van een bepaald land kan zijn, maar een populatie kan ook een deelgroep zijn, b.v. alle mensen die koorts hebben, of hoofdpijn hebben of een combinatie. Een groep mensen waarbij de prevalentie dus hoger is dan bij de totale bevolking.

Eerder had ik het theorema van Bayes al eens besproken toen het over de NIPT-test ging (Het theorema van Bayes en de NIPT-test). Toegepast op een Covid-test ziet het theorema van Bayes er als volgt uit:

De kans op Covid bij een positieve test is de verhouding van de kans op een terecht positief geval (product van sensitiviteit en prevalentie) op de kans op een positief geval bij een gegeven prevalentie. Het theorema van Bayes drukt uit welk gedeelte van alle positieve gevallen terecht is en wat de voorspellende waarde is van de test voor een individuele persoon.

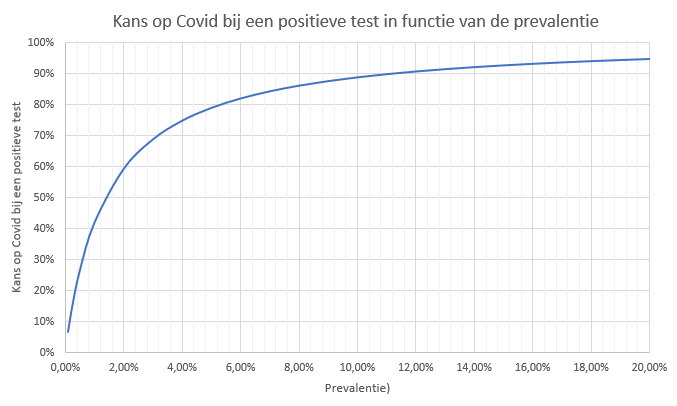
In de onderstaande grafiek is de voorspellende waarde van de test weergegeven in functie van de prevalentie, rekening houdende met een sensitiviteit van 71% en een specificiteit van 99%. Op deze grafiek is duidelijk te zien dat, als we werkelijk iedereen testen bij een prevalentie van 2% (wat we momenteel aannemen voor de totale bevolking), de kans slechts 60% is dat de test terecht is. De aanpak om enkel een risico-groep te testen waarbij de prevalentie hoger ligt stuwt de voorspellende waarde van de test de hoogte in. Bij een prevalentie van 20% (dat wil zeggen een risico-groep waarbij per 100 personen er 20 besmet zijn met het virus) is duidelijk te zien dat de voorspellende waarde stijgt naar 95%.

Besluit is alleszins dat het geen enkele zin heeft om met de test die er nu is een gehele bevolking te testen, de meeste mensen behoren immers niet tot een verdachte groep. Uiteraard zijn niet alle parameters exact bekend. Er wordt getest om de prevalentie te meten, en de voorspellende waarde is afhankelijk van die prevalentie. Daarnaast is ook de specificiteit een schatting. Maar een ruwe schatting is in dit geval veel beter dan niets! Het blijft dus een combinatie van wiskunde en gezond verstand.

Waarom testen we niet gewoon iedereen? Daarom dus!

Terecht positieve groeten,

T.E.