De aanwezigheid van een bucolisch kabbelend beekje met wat keien en stenen, is voor veel mensen, waaronder mezelf, niet zozeer een aanleiding om mediterend de intrinsieke schoonheid van de natuurpracht tot zich te nemen, maar eerder een uitnodiging om deze natuurlijke elementen te gaan verbouwen tot een dam of, in casu, tot een oeververbindende boogbrug. Het gevecht tegen de zwaartekracht mondde daarna dan toch uit in een quasi oeverloze meditatie over de ideale boogvorm.

Waarom blijft de ene boog staan en stort de andere boog ter aarde? Om het antwoord op deze vraag te vinden beschouwen we de krachtwerking in een boog. Wanneer de boog is opgebouwd uit losse stenen zijn de enige krachten die doorgegeven kunnen worden drukkrachten tussen de stenen. In een geïdealiseerd model kunnen we stellen dat de richting van de kracht in de boog telkens precies evenwijdig moet zijn aan de vorm van de boog (een raaklijn van de boog). Daarenboven dient die kracht op ieder punt de resultante te zijn van de verticale kracht, afkomstig van het eigen gewicht van de ontwikkelde booglengte, en de horizontale drukkracht in de boog. Er is slechts één curve die erin slaagt om dit huzarenstukje tot een goed einde te brengen. Maar we maken eerste een zijstap naar een analoge situatie waar de drukkrachten trekkrachten worden.

De unieke eigenschap van de perfecte boog waarin enkel drukkrachten spelen heeft z’n analogie in de kettinglijn waar enkel trekkrachten mogelijk zijn. Dit zorgt ervoor dat de kettinglijn het perfecte spiegelbeeld is van de gezochte boogvorm. Anders dan bij een boog dient zij niet in de juiste vorm gebouwd te worden, maar valt deze automatisch in de juiste vorm, dankzij de zwaartekracht. Dit is een toestand van minimale potentiële energie, dat is een professionele uitdrukking voor iets dat gewoon hangt te hangen of gevallen is. Gaudi heeft handig gebruik gemaakt van deze analogie door te steunen op een model met hangende touwen voor het ontwerp van z’n Sagrada Familia.

Het antwoord op de perfecte boogvorm vinden we bijgevolg door een blik te werpen op de vorm van een kettinglijn. Deze vorm vinden we terug bij halskettingen of hoogspanningskabels. Aan de lezer de keuze welke van beide hij aandachtig wenst te bestuderen. Al heel wat befaamde wetenschappers hebben hun tanden stuk gebeten op het bepalen van de exacte curve van de kettinglijn. Zo veronderstelde Galileo dat dit een parabool betrof, al wist hij dat het eigenlijk een benadering betrof (het idee van heliocentrisme had hij wel goed). Het was Jakob Bernoulli die op het einde van de 17de eeuw enkele wiskundigen uitdaagde om de juiste vorm exact af te leiden en uiteindelijk werd de oplossing in 1691 gepubliceerd door Christiaan Huygens, Gottfried Leibniz en Johan Bernoulli. Driewerf hoera voor deze heren! Maar welke formule schuilt nu achter de kettinglijn? Onze zoektocht zal nu even in wiskundewonderland passeren, maar eerst willen we ons verwonderen over de kroonzaal van het paleis in het historische Ctesiphon (huidige Irak), waarvan de vorm van de boog een bijna perfecte kettinglijn is, en dat is meteen de verklaring waarom deze constructie nog steeds overeind staat (zie afbeelding hieronder). Een knap staaltje Perzische engineering uit de 3de eeuw, van lang voor de tijd van de heren Huygens, Leibniz en Bernoulli.

In de onderstaande figuur is een stuk kettinglijn beschouwd tussen punt A en B. In punt A is er enkel een horizontale kracht T₀ aanwezig want de raaklijn aan de curve in het laagste punt is horizontaal. In het punt B is de trekkracht T rakend aan de curve. De horizontale component van de kracht is T₀ en de verticale component is gelijk aan het gewicht van de ketting tussen A en B. Waarbij λ de massa is per kettinglengte, g de valversnelling en s de booglengte tussen A en B. Hieruit volgt dat de verticale component in het punt B gelijk is aan λgs. Hierdoor kan er een uitdrukking gevonden worden voor de tangens van de hoek θ, dat wiskundig gezien ook gelijk is aan de afgeleide van de curve:

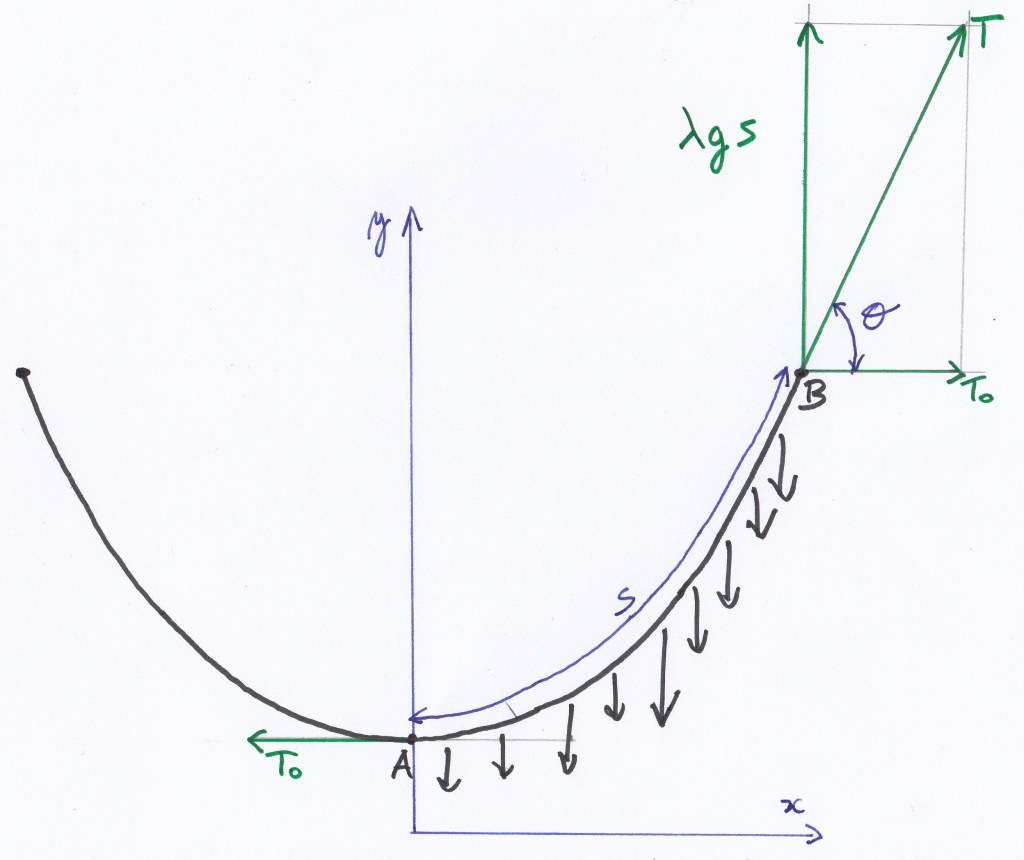
Als we de verhouding van de horizontale kracht en het gewicht per lengte voorstellen door een parameter a:

kunnen we het verband tussen de booglengte s en de helling van de curve op de volgende manier noteren:

Het afleiden van bovenstaande uitdrukking naar x geeft het verband tussen de kromming van de curve en de toename van de booglengte in de x-richting.

Fysisch betekent het dat een toename van de booglengte, dus van extra gewicht zal aanleiding geven tot een kromming van de curve, dat is logisch want de verticale component van de trekkracht wordt telkens groter bij toenemende booglengte, waardoor een kromming ontstaat gezien de horizontale kracht constant T₀ blijft.

Dit lijkt nog een redelijk eenvoudige uitdrukking, maar de booglengte moet nog uitgedrukt worden in functie van x en y. We maken dankbaar gebruik van de stelling van Pythagoras (toegpast op ds, dx en dy) en vinden een differentiaal vergelijking die opgelost moet worden om de ware aard van de kettinglijn te ontrafelen:

Vooraleer we de oplossing uit onze toverhoed halen, kunnen we nog even de vergelijking nader beschouwen. Wanneer de helling heel groot wordt (bij grote waarden van x) zal de vergelijking zich vervellen tot een eenvoudige eerste orde differentiaalvergelijking waarbij de oplossing een exponentiële functie is, maar voor grote negatieve waarden van x moet dit ook zo zijn, want de kettingfunctie is immers symmetrisch. Zou het dan zo eenvoudig zijn dat het resultaat het gemiddelde is van een positieve en een negatieve exponentiële functie? Inderdaad! En de som van deze exponentiële functies kan ook geschreven worden als een cosinus hyperbolicus.

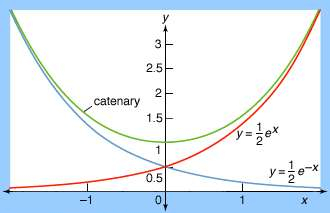
Dus hoogspanningskabels, halskettingen en touwen hebben allemaal de vorm van een cosinus hyperbolicus. (De naam hyperbolicus is trouwens een gevolg van de mogelijkheid om een hyperbool te beschrijven door parametrisatie met hyperbolische functies, analoog aan de parametrisatie van een cirkel met sinus en cosinus) En bijgevolg is de perfecte boog ook een omgekeerde cosinus hyperbolicus, waarbij de parameter a de verhouding van de horizontale drukkracht en het gewicht van de booglengte is. Hoe groter de horizontale drukkracht hoe platter de boog.

Maar als de kracht in de boog varieert, varieert ook de spanning van in het materiaal. Daarom zien we in de praktijk veel boogbruggen die massiever zijn aan de steunpunten dan in het midden. Maar hierdoor verlaten we de wiskundige voorwaarden om te komen tot een kettinglijn. Een bekend voorbeeld van een ‘gewogen kettinglijn’ is de 192 m hoge Gateway Arc in St. Louis (hieronder afgebeeld). Het is een ‘afgeplatte kettinglijn’ omdat het gewicht per booglengte niet constant is.

Is de vorm van de kabel van een kabelbrug dan misschien een kettinglijn? Dat zou logisch lijken. Maar ook hier is het gewicht niet gelijk verdeeld over de lengte van de boog omdat het wegdek dat relatief gezien veel zwaarder is dan de kabel hangt aan de kabel. Hierdoor zal de kabel de vorm krijgen van een parabool en niet van een kettinglijn. Maar wanneer de kabel bij constructie wordt opgehangen zal deze wel een kettinglijn vormen. Naarmate het brugdek wordt gebouwd evolueert de kabel zich tot een parabool.

Kettinglijnen hebben soms onverwachte toepassingen. In het minder voor de hand liggende geval van voertuigen met vierkante wielen is het aangewezen om deze te laten rijden op een wegdek dat precies de vorm heeft van opeenvolgende kettinglijnen. Dit wordt hieronder geïllustreerd door een prof die met vierkante wielen over een wegdek rijdt dat opgebouwd is uit kettinglijnen. Hij rijdt zonder schokken want de wielassen volgen een horizontale lijn.

Een ruimtelijke figuur die wordt bekomen door een kettinglijn te roteren rond de x-as wordt een catenoïde genoemd. Een speciale eigenschap van een catenoïde is dat het een minimaaloppervlak is, wat betekent dat een catenoïde het minste oppervlak nodig heeft om de gegeven randvoorwaarden te verbinden in de ruimte. Een zeepbel gevormd tussen twee cirkels is een mooi voorbeeld hiervan.

Een ander voorbeeld van een catenoïde is de vorm van het beschermdoek van sommige trampolines met cirkelvormige randen boven en onder. Dit ontdekte ik toen ik een aantal dagen geleden vanuit de tuin van de buren even verder naar mijn eigen tuin keek en me plots de vorm van het beschermingsdoek opviel. Dit gebeurde juist op het moment dat ik aan het vertellen was dat ik iets wou schrijven over bogen en kettinglijnen! Soms is het echt verrijkend om eens iets vanuit een ander perspectief te bekijken. En dat is wellicht niet enkel geldig voor trampolines…

hyperbolische groeten,

T.E.