Geplaatst op door Tijs Essel · 1 reactie

De derailleur dirigeert de dans van tandwielen en trapcadans

Wanneer er een belangrijke wielerwedstrijd is, zoals het WK, wil ik ook altijd met een zeker fietsgevoel voor de tv zitten en daarom ga ik in de voormiddag meestal een toertje doen. Omdat ik onlangs een beugel heb geïnstalleerd om m’n fiets omhoog te hangen (dat hoort zo in een georganiseerde garage), keek ik net voor ik m’n fiets van de haak haalde recht naar de derailleur: een knap staaltje techniek dat ervoor zorgt dat je in een comfortabele cadans kan rijden. Wind tegen, bergop, met de wind mee of bergaf. Altijd het juiste verzet.

cassette

Het woord derailleur is onlosmakelijk verbonden met de fiets, niemand zal zeggen dat hij miserie heeft met de derailleur van z’n auto. Het woord ‘derailleur’ klinkt ook net alsof je een ketting hoort rollen over tandjes. En als je het woord ‘derailleur’ laat vallen lijkt het direct of je een ervaren rot in het wielrennen bent. Het komt uit de tijd dat het Frans nog de lingua franca was in het fietswereldje, en als ik menig fietshersteller of de televisiecommentator hoor is dat nog steeds zo. Zo rem je met je ‘frein’ en als je op de borduur rijdt moet je opletten voor je ‘janten’. En ‘coureurs’ die ‘demarreren’ uit het peloton moeten opletten dat ze geen ‘chasse patate’ doen. Alhoewel, ik ben niet helemaal zeker of Voltaire deze uitdrukking frequenteerde.

‘Een tandje bijsteken’ is een wijdverbreide uitdrukking die gebruikt wordt wanneer er nog net dat ietsje inspanning meer nodig is of gevraagd wordt. Om dat tandje bij te steken heb je een derailleur nodig, en ironisch genoeg maak je het jezelf gemakkelijker wanneer je achteraan een tandje bijsteekt en het spreekwoord preciseert niet de ligging van het tandwiel. Dringend tijd om eens na te gaan hoe dat nu juist zit. De bedoeling is dat je met je pedalen een aangename trapfrequentie kan trappen, bv. 90 RPM (rounds per minute).

Het verzet is de afstand die je aflegt met één trapomwenteling, dus bergop en tegen wind hebben we een klein verzet nodig en wind achter of bergaf hebben we een groot verzet van doen. Wanneer we vooraan en achteraan evenveel tandwielen hebben dan is het verzet gelijk aan één wielomtrek. Bij een normale koersfiets is dat 2,1 m. Het aantal tandwielen voor en achter maakt niet uit, enkel de verhouding van beide. Daar voelen we inderdaad al een formule opkomen. Als we vooraan dubbel zoveel tandjes hebben als achteraan, dan zal het achterwiel 2 keer moeten draaien bij één predaalomwenteling. In dat geval is het verzet het dubbele van de wielomtrek, dus 4,2 m. Algemeen kan men dus stellen dat:

Ik heb zonet tandjes zitten tellen op de tandwielen van mijn koersfiets en mijn grootste verzet wordt bepaald door het grootste tandwiel voor (53) en het kleinste achter (12):

Als je dat verzet ronddraait met een trapfrequentie van 100 RPM dan heb je (in theorie) het werelduurrecord van sir Bradly Wiggins (54,526 km) gebroken, als je die snelheid tenminste één uur zou volhouden.

Wiggins reed trouwens z’n uurrecord met een versnelling 58/14. Verbazend, want dat is een kleiner verzet dan mijn grootste verzet: 58/14 is goed voor een verzet van 8,7 m. Hij zal dus met een trapfrequentie van ca. 105 RPM gereden hebben.

Sir Bradley Wiggins - UCI Hour Record Attempt

Maar er is meer! Want de derailleur zorgt er voor dat je voor en achter kan kiezen uit verschillende tandwielen. Vooraan heb ik twee tandwielen: het grootste heeft 53 tanden en het kleinste heeft er 39. Achteraan heb ik een tandwielcassette met maar liefst 9 tandwielen van groot naar klein: 25-23-21-19-17-15-14-13-12. Mijn kleinste verzet bedraagt dus 39/25 maal mijn wielomtrek wat neerkomt op 3,276m. De verhouding van het grootste en het kleinste verzet wordt het versnellingsbereik genoemd, hier is dit 2,83. Soms wordt dit in procent uitgedrukt: mijn koersfiets heeft een versnellingsbereik van 283% Om een echt groot versnellingsbereik te verwezenlijken heb je 3 tandwielen vooraan nodig,  dan kan je tot 600% gaan.

Ik heb 2×9=18 mogelijke combinaties, maar in realiteit heb ik maar 12 versnellingen omdat een combinatie 53/19 ongeveer hetzelfde verzet geeft als 39/14 zie ook onderstaande tabel, met in het groen de 12 effectieve versnellingen. Het leidt geen twijfel dat het verschil tussen combinaties en versnellingen al meermaals geleid heeft tot hoogoplopende caféruzies en misverstanden. In het genre van: ‘Wat zeg je? Ik heb geen 24 versnellingen? Kijk maar eens naar mijn fiets: 3 vooraan en 8 achteraan! Het kleinste kind kan dat toch zien?’. ‘Ja maar kijk eens naar uw verzet-tabel’. ‘Ik zal eens een verzet-tabel steken…’ Enzovoort, enzovoort…

verzettijs

Als we de verzetten van de 12 versnellingen uitzetten per versnelling dan zien we dat deze geen lineair verloop kennen. Dat is logisch want de verhoudingen tussen de opeenvolgende verzetten moet zo gelijk mogelijk zijn en niet de verschillen in verzet. Tiens, dat doet me denken aan de gelijke ratio tussen de frequenties van gelijke intervallen (zie: Alle piano’s zijn een beetje vals). De verhoudingen zijn hier geen verhoudingen van frequenties, maar verhoudingen van verzetten. De wiskunde achter beide fenomenen is krak hetzelfde.

We zoeken dus de gemiddelde ratio waarmee we 11 keer het kleinste verzet (3,276 m) kunnen vermenigvuldigen om uit te komen bij het grootste verzet (9,275):

Hieruit volgt:

Voor de lol zullen we dit eens uitrekenen met logaritmes (in dit geval met Briggse logaritmes met basis 10, maar dit mogen gerust ook Neperiaanse logaritmes zijn – voor iemand me beschuldigt van favoritisme)  zodat de machtsverheffing een vermenigvuldiging wordt, daarvoor gaan we linker- en rechterlid naar het parallelle universum van de logaritmes sturen:

Hieruit volgt:

En dus is de gemiddelde ratio:

Gemiddeld zal dus iedere versnelling een verzet hebben dat 10% hoger ligt dan de vorige versnelling. Maar het aantal tanden zijn discrete waarden, dus moet er een combinatie gezocht worden die zo dicht mogelijk bij de gemiddelde ratio ligt. Hieronder zijn de verzetten uitgezet ten opzichte van de verzetten bij gelijke ratio. Je kan duidelijk zien dat de ontwerper van mijn versnellingen zijn best gedaan heeft om zo dicht mogelijk aan te sluiten bij de curve van gelijke ratio’s, zodat iedere versnelling aanvoelt als een even zware relatieve verhoging van het verzet. Wat me ook weer doet denken aan de exponentiële constante groei uit: Dromen over het getal e, want we verkrijgen ook hier een exponentiële curve, zie ook onderstaande grafiek.

versnellingentijs

Maar als je het uurrecord wil breken, mag je dit allemaal vergeten, want dan hoef je maar één verzet te voorzien… En trappen maar!

Je zal al snel merken dat Wiggins een ongelofelijke prestatie heeft neergezet… ik probeer alvast bij een volgend fietstochtje eens één minuut de uurrecordsnelheid van Wiggins aan te houden. Ik kan het alleszins al niet meer steken op mijn verzet…

Ik heb door deze vernieuwde inzichten in de werking van mijn derailleur warempel zin gekregen om als de wiedeweerga mij stalen ros te bestijgen!

Sportieve groeten,

T.E.

Geplaatst op door Tijs Essel

Het geheim van de dubbele regenboog

Na zondvloed komt regenboog. Het zou een oude weerspreuk kunnen zijn, die wellicht toch in ongebruik zou geraakt zijn wegens de lage frequentie aan Genesis-zondvloeden. Sinds mensenheugenis is de fascinatie voor de zevenkleurige hemelboog met overtreffende adjectieven beschreven, getekend en bezongen. De dubbele regenboog die hier afgebeeld is ontving ik van het kampverslag van stamina, en bezorgde mij ook deze keer weer verwondering, verrukking en inspiratie.

Dubbele regenboog

Niemand minder dan Isaac Newton zorgde voor de ontrafeling van de regenboog in z’n werk ‘Opticks’. Alle wonderlijke verhalen en voortekenen die in het pre-Newtontijdperk aan een regenboog werden toegedicht werden abrupt verstoort door de ontluisterende theorie over de breking van het licht. Door de breking van het licht werd het mysterie van de regenboog gebroken. Jammer vinden misschien sommigen, maar persoonlijk vind ik dat we van Newton een mooi geschenk hebben gekregen. We waren blind. En nu kunnen we zien!

Newton was een ongelofelijk fenomeen, die we natuurlijk vooral kennen door de wetten die naar hem genoemd zijn over de principes van de klassieke mechanica. Hij doorzag dat appels die van bomen vallen en de maan die rond de aarde draait beide effecten zijn van hetzelfde fenomeen. Hij kon zich uren-, dagen-, maandenlang intens concentreren op een probleem. Hij was bijgevolg niet iemand die gezelligheidsbezoekjes op prijs stelde… Het zeldzame bezoek werd vaak volledig aan z’n lot overgelaten toen Newton plots een inval kreeg en naar z’n kamer trok om die even verder uit te werken, gedurende enkele uren… En o ja, hij vond ook nog eens het integraalrekenen uit! Ik zou hem nu erg kunnen jennen door te suggeren of dit misschien Leibniz niet was… z’n vetes met Leibniz en andere wetenschappers zijn legendarisch.

En dat deed hij allemaal tussen de soep en de patatjes want eigenlijk was hij grote delen van z’n tijd bezig met theologie. Zo had Newton na lange en intense bijbelstudie problemen met de goddelijke drievuldigheid, en dat was nogal onhandig omdat hij werkte op het Trinity College. Even analytisch als z’n ander werk had hij een lijstje opgesteld met 12 punten waarmee hij aantoonde dat de drie-eenheid van God een miskleum was, ongelukkigerwijs dogmatisch ingevoerd door enkele kerkvaders in de derde eeuw na christus omdat een God de Vader, een God de Zoon en nog een God de Heilige Geest niet compatibel waren met een monotheïstische godsdienst.

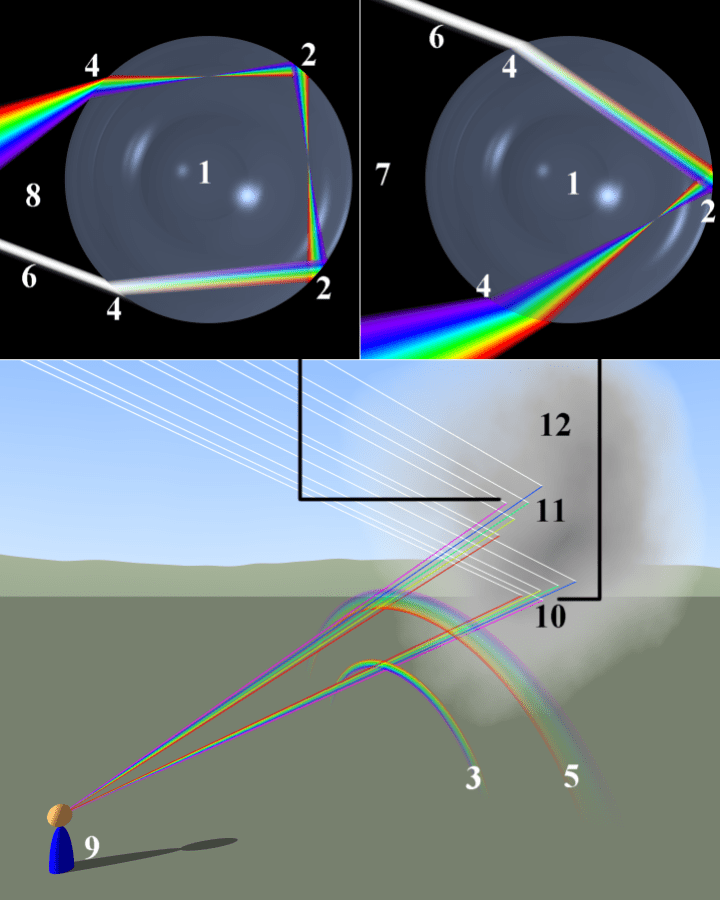
Newton doorzag dus ook het licht. Hij liet een fijne straal licht binnen en bestudeerde de breking ervan door een prisma. En zoals het witte licht gebroken wordt door een prisma wordt het ook gebroken door een regendruppel. De lichtsnelheid in lucht en in water is verschillend. In water is de snelheid slechts drie vierde van de lichtsnelheid in lucht. In diamant gaat het licht nog veel trager, vandaar de vele schitteringen in diamant.

Er is nu nog één ding die je moet weten om het totale plaatje te begrijpen. De verschillende frequencies van licht hebben een verschillende brekingsindex (verhouding van snelheid in vacuum ten opzicht van de lichtsnelheid in een materiaal), daarom schieten ze elk naar buiten onder een verschillende hoek en daarom zie je dus een regenboog. De kleuren gaan elk hun eigen weg, zoals ze elk hun eigen snelheid hebben.

En waarom zie je soms een dubbele regenboog, waarvan de tweede lichter van intensiteit is in omgekeerde kleurvolgorde? Dat is in feite redelijk simpel. De hoofdregenboog wordt gevormd door het licht dat aan de bovenzijde van een druppel binnendringt en één keer weerkaatst wordt op de achterzijde vooraleer het terug naar buiten treedt. De tweede regenboog wordt gevormd door licht dat langs de onderzijde binnendringt in een druppel en tweemaal weerkaatst wordt op de achterzijde. Door deze extra weerkaatsing is de kleurvolgorde omgekeerd. En doordat het tweemaal wordt weerkaatst is de intensiteit veel minder. Hieronder is het nog eens mooi in een tekening weergegeven:

Rainbow_formation

Voor degenen die het toch jammer vinden dat de regenboog gedemystificeerd is door toedoen van Newton zoals een goocheltruk die uitgelekt is kan ik de vraag voorleggen die ik onlangs las ergens in ‘De vliegeraar’ van Khaled Hosseini: ‘Wil je liever getroost worden door een leugen dan gekwetst worden door de waarheid?’

Hit me Newton one more time!

Rode, oranje, gele, groene, blauwe, indigo en violette groeten,

T.E.

Opticks

Geplaatst op door Tijs Essel

Een koperen bol om de treinen stipter te laten rijden

Soms zie je toeristen naar boven kijken op plaatsen waar je altijd gewoon passeert en meestal zal het je worst wezen waar ze naar staan te kijken, maar deze keer volgde ik hun blikken en zag bovenop het gebouw ‘Bouchoute’ op de Grote Markt van Brugge een koperen bol staan. Blijkbaar had een astronoom, Alphonse Quetelet, deze bol daar laten plaatsen. De bedoeling was de treinen stipter te laten rijden.

20180909_161540

De stiptheid is blijkbaar al van sinds het prille begin van het treinreizen een heuse bekommernis die zwaar genoeg woog om er een astronoom voor in te schakelen. In die tijd liepen de lokale tijdsbepalingen nogal uiteen, want alle steden en dorpen bepaalden zelfstandig was de juiste tijd was. Blijkbaar was dit geen exacte wetenschap want de lokale tijd kon soms tot een klein halfuur verschillen… en dat leidde tot problematische dienstregelingen.

Stel je een trein voor die vijf na tien vertrekt en vijf voor tien toekomt in het volgende dorp, dat is natuurlijk niet echt een handige situatie. Daarom moest de tijd overal waar er belangrijke stations waren zo nauwkeurig mogelijk bepaald worden. En dat deed men aan de hand van een soort zonnewijzer, want de koperen bol wierp een schaduw op de Grote Markt en wanneer het middag was passeerde die schaduw voorbij een lijn, de meridiaan.

De toeristen waren net als een zonnebloemveld waarbij elke bloem reikhalzend zoveel mogelijk zonnelicht en -warmte wil ontvangen. Maar toen leek het alsof de duisternis in enkele luttele seconden was nedergedaald en Helios z’n zonnewagen plots short-cut-gewijs de dieperik instuurde want plots richtte het zonnebloemveld der toeristen hun blik naar beneden. En toen zag ik het ook.

20180909_161548

Als een soort knopenrij waarmee de markt z’n kasseimantel dicht houdt om zich te beschermen tegen de scherpe stalen wielen van de koetsen en de onbeschaamde blikken van de vele passanten zijn in een min of meer mooie rechte rij een grote hoeveelheid koperen nagels geplaatst. Dit is de meridiaan! Wanneer de schaduw van de koperen bol precies op deze lijn lag, zette iedereen z’n klok gelijk op stipt twaalf uur. Toen maakte men zich nog geen zorgen over zomer- en winteruur…

De machinist met de klok diende zich dan enkel nog te elfder ure te spoeden naar het station dat zich een Steenstraat verder bevond op ’t Zand. Het allereerste stationsgebouw die daar gebouwd is 1844 zal je daar in de verste verte niet meer vinden, maar wil je het toch eens bezoeken dan kan dat simpel, want het eerste stationsgebouw van Brugge staat nu in Ronse.

“Toet zei de trein en de statie ging vooruit”, een zinsnede die ik dikwijls hoorde in mijn kindertijd blijkt nu toch enige waarheid te bevatten. Dat zal mijn pa graag horen.

Met stipte groeten,

T.E.

Brugge eerste station op zand

Het eerste station van Brugge op ’t zand…

1280px-Ronse_-_Station_1

…en toen Brugge het niet meer nodig had, werd het geadopteerd door Ronse.

Geplaatst op door Tijs Essel · 2 reacties

Schaakmat voor koning Shirham

1280px-Wheat_and_chessboard_problem

Wie was niet graag een vlieg op de muur geweest op het moment dat de raadslieden van de Indiase koning Shirham hem, nadat zij verbijsterd hun berekeningen verschillende malen hadden nagezien, voorzichtig kwamen melden welke exacte hoeveelheid graan de vorst in al z’n enthousiasme had beloofd aan de geniale en gewiekste uitvinder van het schaakspel? 

Toen de koning wat aangedrongen had om een gepaste beloning voor te stellen, had die laatste quasi achteloos gevraagd om hem één graankorreltje te schenken op het eerste vakje van het schaakbord, twee graantjes op het tweede vak, 4 op het derde vak, vervolgens 8 op het vierde vak, enzovoort… tot aan vakje 64. Koning Shirham dacht aan de enorme koninklijke graanschuren en het leek hem niet onoverkomelijk om de ogenschijnlijk bescheiden man te belonen met een aantal zakken graan, maar was zich niet bewust geweest van de kracht van een exponentiële groei. Integendeel, hij worstelde met de gedachte of hij zich niet beledigd moest voelen met de peulschil die gevraagd werd voor zo’n prachtig spel.

Met welk getal kwamen de raadslieden zenuwachtig schoorvoetend  naar binnen schuifelen? Het was hen waarschijnlijk opgevallen dat alle termen van de som machten van 2 zijn. De som S die we hier zoeken ziet er als volgt uit:

Ja inderdaad: 2 tot de nulde macht is 1 (elk getal tot de nulde macht is trouwens één). Louter ter info is ook de sommatie-notatie toegevoegd, want wiskundigen drukken zich graag beknopt uit. Om te weten te komen hoeveel S is, zoeken we eerst hoeveel het dubbele zou zijn van de som. Dit kan gemakkelijk door bij iedere term de exponent eentje te verhogen:

Als we nu het verschil maken van 2S en S dan bekomen we de volgende eenvoudige uitdrukking voor de som:

Als we dat uitrekenen op een rekenmachine die genoeg cijfertjes toelaat komen we op 18 446 744 073 709 551 615 graankorreltjes.

“Zijne hoogheid heeft mijnheer de bedenker van het schaakspel achttien triljoen vierhonderdzesenveertig triljard zevenhonderdvierenveertig biljard drieënzeventig miljard zevenhonderdennegen miljoen vijfhonderdeenenvijtig duizend zeshondervijftien graankorrels beloofd”, sprak de moedigste der raadslieden. De koning zal wellicht al wat nattigheid gevoeld hebben, maar hoopte alsnog dat het ging over een uit de kluiten gewassen karrevracht graan. Ach, het ging dan ook over de uitvinder van het schaakspel…

We waren helaas niet de vlieg op de muur, maar het zou best kunnen dat één der raadslieden het wat aanschouwelijk probeerde te maken voor zijn koning, waarvan de gezichtuitdrukking liet verstaan dat hij het in Keulen hoorde donderen, en de volgende woorden sprak: “Hoogheid, dat is een graantapijt van één voet hoog over de volledige oppervlakte van uw rijk.” Waarbij we er even voor het gemak van uitgegaan zijn dat zijn rijk even groot was als het huidige Indië, pakweg 144,5 miljoen vierkante kilometer vaderland. In die tijd was de afstand tot de dichtste ster Proxima Centauri nog niet geweten, maar de raadslieden hadden de koning ook kunnen doen duizelen door te stellen dat de totale lengte van alle gevraagde graankorrels in een rij voldoende was om de afstand tot aan die ster te overbruggen… en terug.

Naargelang de versie van het verhaal werd de uitvinder stante pede onthoofd, of tot hoogste adviseur van de koning benoemd. Maar in geen enkele versie mag hij trouwen met de dochter van de koning. In andere legendes is het voldoende om met leeghoofdige viriliteit in het rond te slaan en deze of gene vijand of vijandelijk dier te verslaan om de dochter van de plaatselijke monarch te mogen huwen. Maar een geniale mens die nota bene het schaakspel heeft uitgevonden, die blijkt dan toch een beetje teveel nerd voor dochterlief… tss tss.

Zonde! Maar dat was natuurlijk lang voor de tijd dat STEM (Science-Technology-Engineering & Mathematics) populair werd…

T.E.