Geplaatst op door Tijs Essel

Over structuren en vervormingsenergie

Onlangs kon ik aan de lijve ondervinden dat bepaalde structuren niet ontworpen zijn om sterk of stijf te zijn, maar om zoveel mogelijk energie om te zetten in vervorming. Bepaalde structuren zoals een auto… en energie zoals bij een botsing. Botsen is in feite het omzetten van kinetische energie naar vervormingsenergie. Bij uitbreiding is dit geldig voor alle structuren. De vervormingsenergie is altijd gelijk aan de energie of arbeid (kracht maal vervorming) geleverd door de externe krachten.

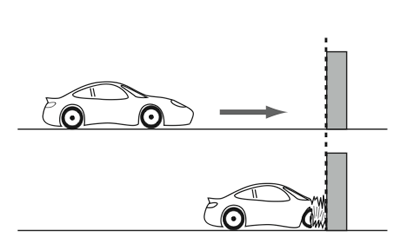
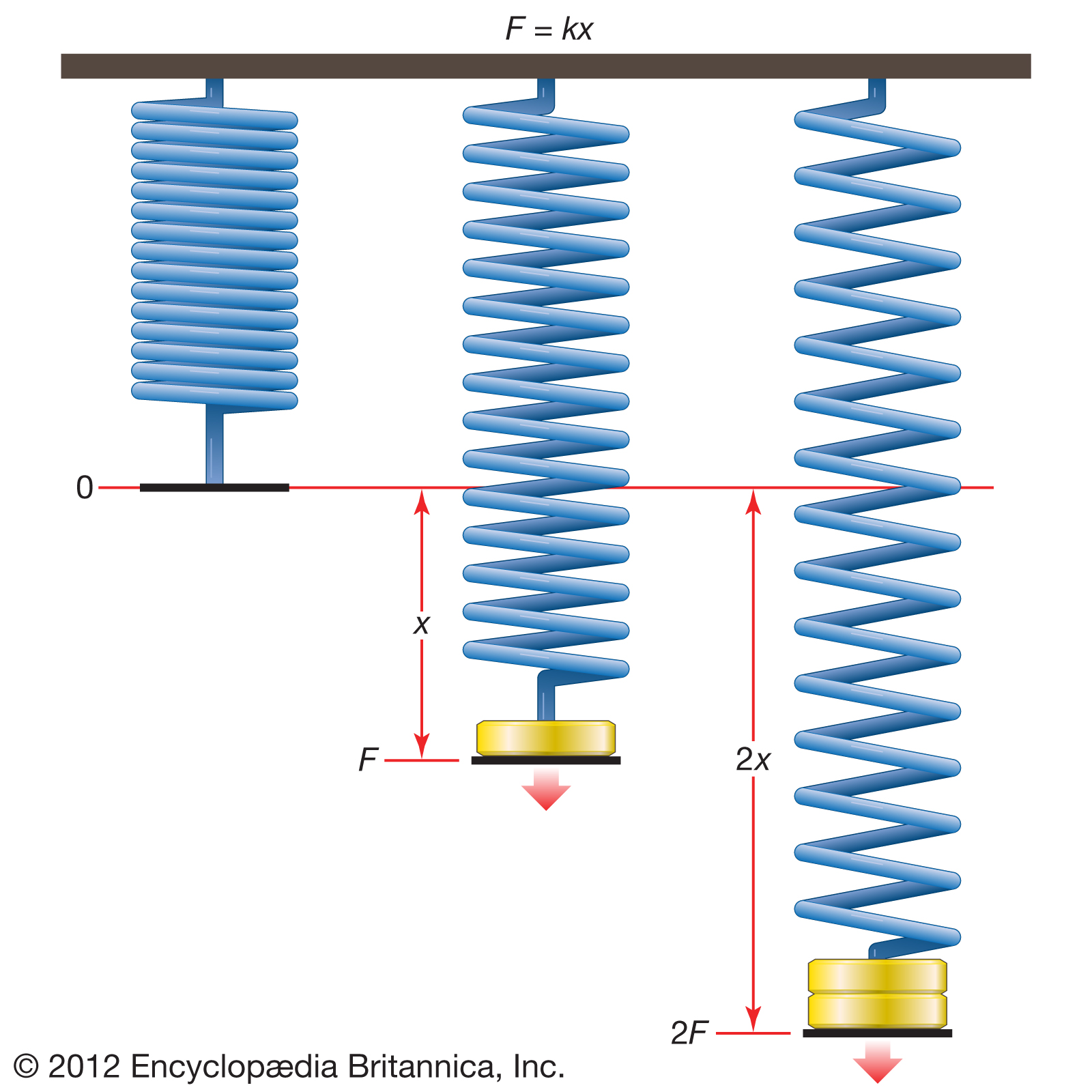
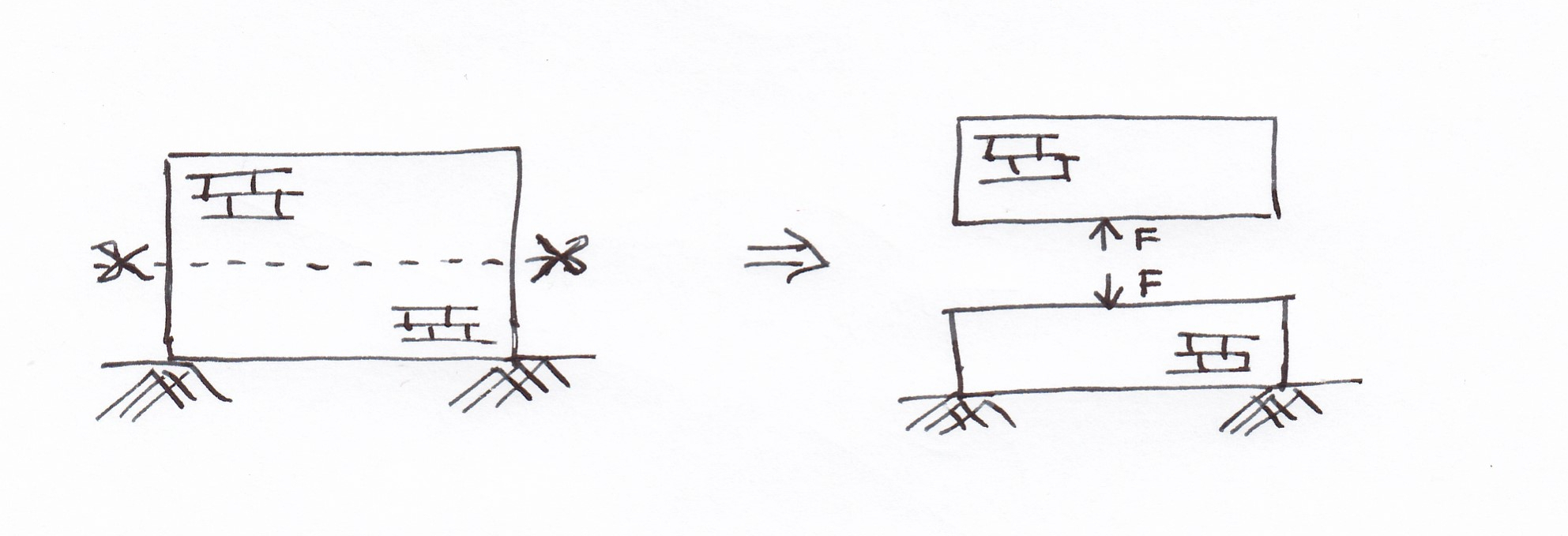
Een auto die tegen een muur knalt is iets spectaculairder dan een normaalkracht op een kolom van een structuur, maar in feite is het qua vervormingsenergie helemaal analoog te beschouwen. We kunnen aannemen dat zowel de auto als de kolom een vervormingsgedrag zullen vertonen dat we kunnen benaderen als lineair elastisch gedrag (zie ook: Over structuren en de wet van Hooke). Bij zware botsingen is de kans echter zeer klein dat de auto weer elastisch naar oorspronkelijke toestand gaat, maar bij een lichte ‘bumperkus’ is de vervorming meestal elastisch. Wanneer de vervorming permanent is en de takeldienst dient gebeld te worden dan hebben we een mooi voorbeeld van plastische vervorming.

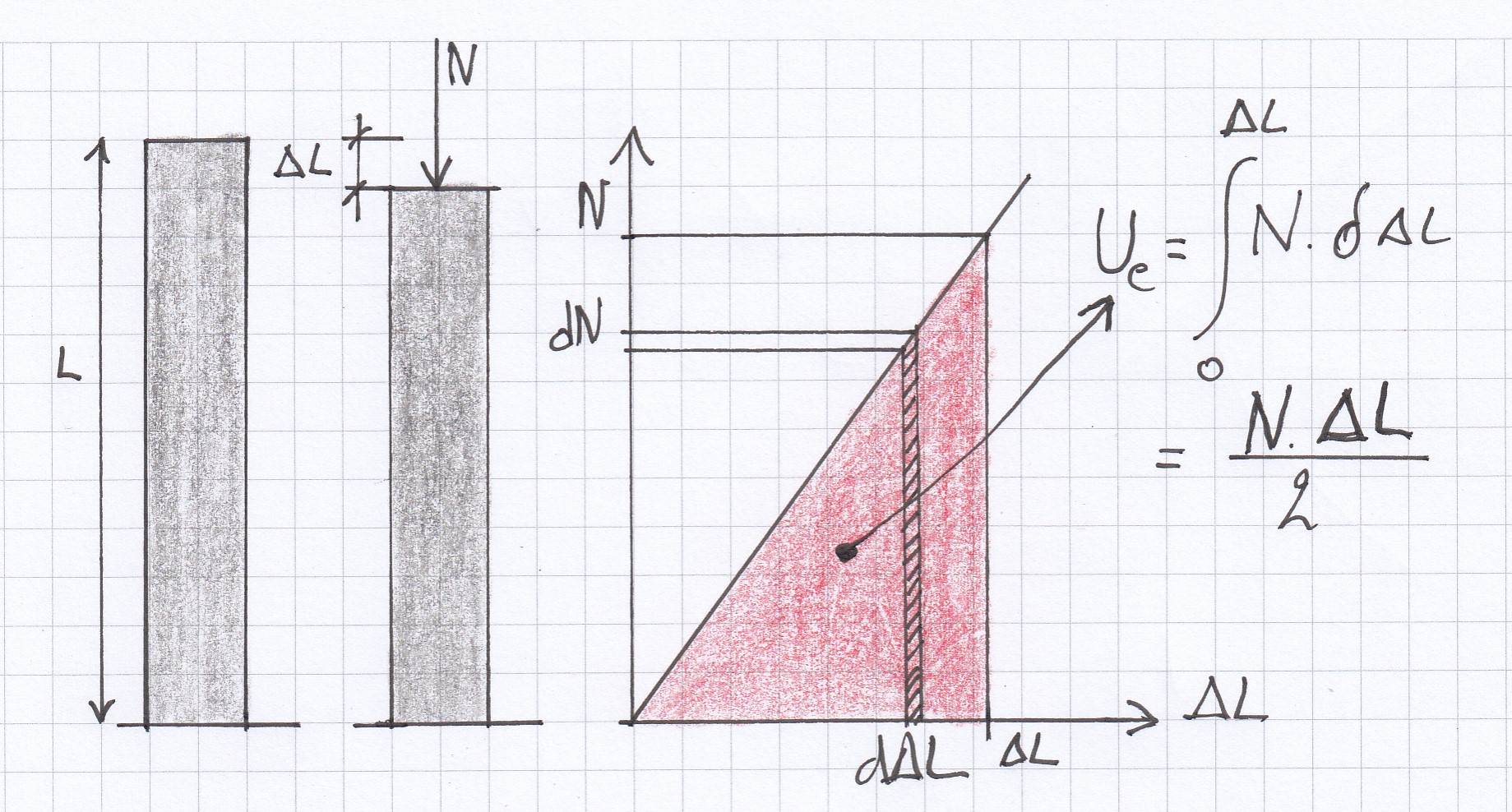
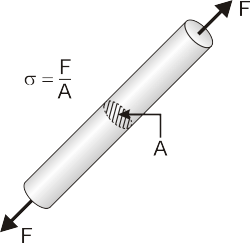
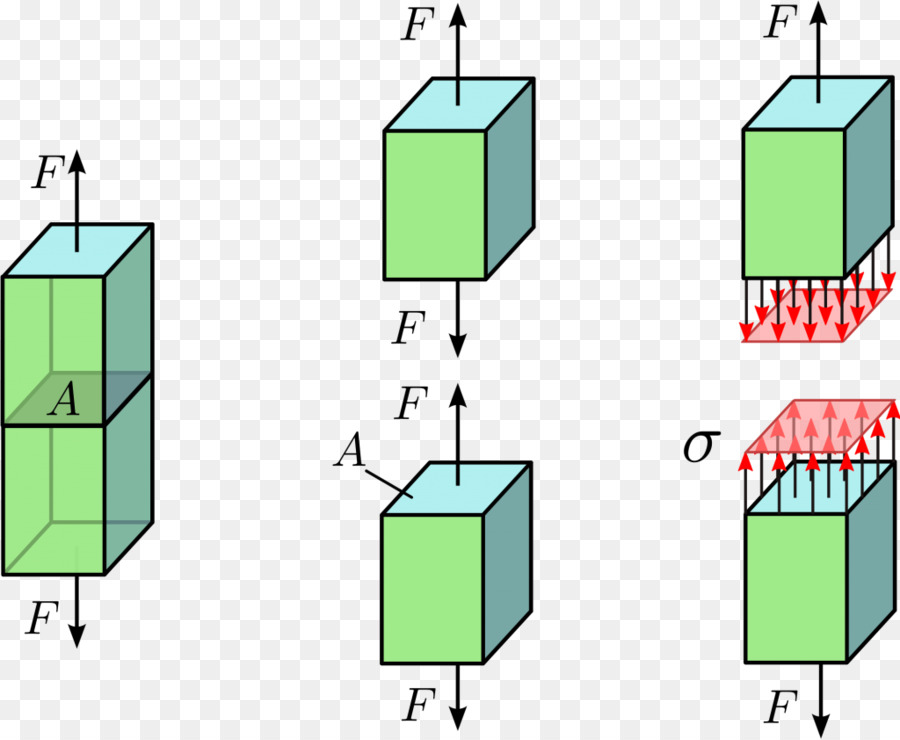
Hoe weten we nu hoeveel vervormingsenergie er zit opgeslagen in een structuur, bijvoorbeeld in de kolom? Om dit te bepalen gaan we een kracht langzaam toenemend laten aangrijpen op de kolom en bij elke extra verkorting berekenen we de arbeid door deze te vermenigvuldigen met de aangrijpende kracht. Het komt er in feite op neer dat de geleverde arbeid gelijk is aan de oppervlakte onder de grafiek waarin de kracht is weergegeven in functie van de verlenging. Wiskundig gezien levert dit een integraal op, maar wat kennis over de oppervlakte van een driehoek is hier voldoende om tot een uitdrukking te komen van de externe arbeid (U) geleverd op de constructie:

arbeid op kolom

De wet van Hooke heeft het volgende verband tussen verkorting en kracht:

Door het bovenstaande te substitueren in de uitdrukking van de arbeid kunnen we de de vervormingsenergie in de constructie uitdrukking in functie van de interne krachten:

Energie is één van de meest fundamentele eenheden in de natuurkunde en een probleem uitdrukken in functie van energie is dan ook een zeer algemene benaderingswijze, waaruit heel veel specifiekere rekenregels voortgekomen zijn. Zeer algemeen gezegd zal een constructie in (stabiel) evenwicht zijn wanneer z’n totale (potentiële) vervormingsenergie een minimum heeft bereikt,  zoals ook een bal rolt naar het laagste punt (het lokaal laagste punt). En als we zoeken naar een minimum, dan is het evident dat de partiële afgeleiden niet ver weg zijn…

Ook al is het streven naar minimum potentiële vervormingsenergie een algemeen streven van alle constructies, het zal in veel gevallen niet de meest eenvoudige manier zijn om te komen tot een bevattelijke en handige structurele analyse. De Italiaanse ingenieur Castigliano ontwikkelde een methode om de interne krachten en de doorbuiging te berekenen van elastische systemen. Hij vond dat de verplaatsing in een bepaald punt van een constructie in verband stond met de partieel afgeleide van de vervormingsenergie naar de bijhorende virtuele kracht die werkt in dezelfde richting van de gezochte verplaatsing, wiskundig uitgedrukt ziet dit er als volgt uit:

De methode onderzoekt dus hoe de totale vervormingsenergie zal veranderen door de impact van een kracht op een plaats, waar er in het echt helemaal geen externe kracht zal aangrijpen. Dit gegeven maakt dat de hele theorie zich niet zo gemakkelijk laat uitleggen in simpele taal en dat er sprake is van ‘virtuele arbeid’, deze wiskundige wereld staat nogal veraf van de bekistingen en de wapening waar een structureel ingenieur dagelijks mee bezig is. Laat ons nu toch maar even Castigliano toepassen op de bovenstaande uitdrukking van vervormingsenergie:

Dat lijkt alvast te kloppen! Het verder in detail uitspitten van deze energiemethode is echter niet mogelijk zonder dat we een heel gamma van formules moeten bovenhalen welke rekening houden met vervormingsenergie door normaalkracht, dwarskracht, buiging en torsie. En algemeen gezien halveert het aantal lezers bij het gebruik van iedere formule… 

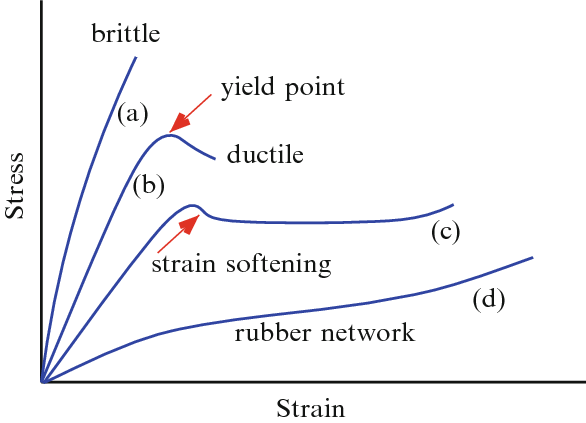
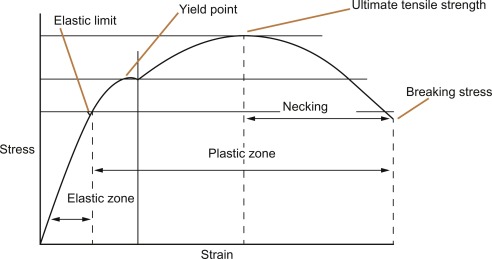
Het equivalent van een botsing voor een auto is een aardbeving voor een gebouw, waarbij een gebouw op korte tijd zeer grote energie moet absorberen. (zie ook: Wat kleuters en hooligans al lang weten over de gevolgen van aardbevingen… ) Zo zal het uiterst belangrijk zijn om te bewaken dat de totale vervormingsenergie die het gebouw kan opnemen voldoende hoog is. Dat kan een geval van leven of dood zijn. Nu we weten dat we de vervormingsenergie gezien kan worden als de oppervlakte onder de spanning-rek-curve is het zeer logisch om te gaan eisen dat er een faalmechanisme moet ontstaan waarbij het staal moet kunnen vloeien en waarbij de ductiliteit (de maximale rek tot breuk, of vervormbaarheid) van het gebruikte staal voldoende hoog moet zijn.

Ook wanneer er geen aardbevingen zijn zal het een groot voordeel zijn wanneer de constructie in grote mate vervormingsenergie kan opslaan vooraleer dat de constructie bezwijkt. Een brug die vervaarlijk begint door te buigen kunnen we nog op tijd ontruimen en ook in een gebouw zal het veiliger blijken wanneer er zich bij overbelasting van bepaalde balken scheuren en overmatige vervorming wordt vastgesteld alvorens zij bezwijken. Daarom is het ook belangrijk dat we een goed zicht hebben op de structuur. cracks-in-beam

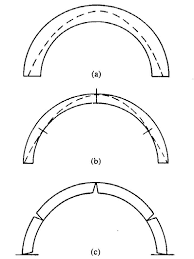
Maar scheuren hoeven niet altijd alarmerend te zijn. Er zijn veel oude gebouwen waarbij er een nieuwe evenwichtstoestand is ontstaan door een scheur, zeker bij boogwerking is dit vaak het geval, deze kunnen nog altijd stabiel zijn door het toevoegen van een scharnier (veroorzaakt door de scheur). Dus blinde paniek bij het vaststellen van scheuren is ook niet nodig.

images

Zoals wijzelf ook liever een waarschuwing krijgen dat onze bloeddruk te hoog is, zodat we dit kunnen genezen, zo is het ook een eigenschap van een goed ontwerp dat de constructie de nodige alarmboodschappen kan uitzenden alvorens te bezwijken. En dan is het natuurlijk wel een kwestie van deze signalen niet te negeren.

Virtuele arbeidsgroeten,

T.E.

Geplaatst op door Tijs Essel · 1 reactie

Over structuren en de wet van Hooke

‘Ut tensio sic vis’, zo klinkt de wet van Hooke in het Latijn. Zoals de verlenging is, zo is de kracht. Het drukt uit dat er een evenredigheid is tussen de kracht op een voorwerp en de verlenging. Denk maar aan een veer van een weeghaak. Bij het verdubbelen van de last zal ook de verlenging verdubbelen. De wet van Hooke stipuleert dat alle materialen zich op deze manier gedragen. Een mooie wet, alleen… geen enkel materiaal volgt deze wet!

kx-law-Hooke-F-force-length-displacement

De wet van Hooke kan men ternauwernood een wet noemen, toch zeker in vergelijking met de quasi algemeen geldende natuurwetten van Newton, z’n eeuwige rivaal. De relatie wordt tegenwoordig echter steeds uitgedrukt als een evenredigheid tussen de spanning (zie Over structuren en het spannend verhaal van trekken en duwen) en rek, wat niet de verlenging is maar de relatieve verlenging. Deze begrippen waren nog niet zo vertrouwd in de tijd van Hooke. De wet van Hooke ziet er dan dus als volgt uit:

Maar zoals reeds aangekondigd zijn er geen materialen die zich perfect houden aan deze wet. Alleen al om de simpele reden dat geen enkel materiaal oneindig sterk is. Ieder materiaal heeft z’n specifieke spanning-rek curve maar één ding is zeker: op een zeker moment is er een breuk. Op onderstaande grafiek is het duidelijk dat er bij kleine rekken een lineair gedrag is, dat is het elastisch gebied, maar verder hebben verschillende materialen uiteenlopend gedrag bij oplopende rek, zoals je op onderstaande grafiek kan zien.

Typical-stress-strain-curves-of-polymers-tested-at-different-temperatures-curves-a-c

De rek. Daar moeten we het eerst eens over hebben. Thomas Young deed ooit een vergeefse poging om dit aan de mensheid uit te leggen, jammer genoeg was er geen enkele sterveling op aarde die een jota begreep van wat hij juist bedoelde… “We may express the elasticity of any substance by the weight of a certain column of the same substance, which may be denominated the modulus of its elasticity, and of which the weight is such, that any addition to it would increase it in the same proportion as the weight added would shorten, by its pressure, a portion of the substance of equal diameter.” Toch wordt de elasticiteitsmodulus naar hem genoemd: de Young-modulus.

Hier volgt mijn poging om het bevattelijk uit te leggen: Rek is de mate van relatieve verlenging of verkorting van een materiaal. Wiskundig gezien is een verkorting een negatieve rek, soms wordt ook wel een het begrip stuik gebruikt om een verkorting aan te duiden. De algemene definitie van rek is de verhouding van de verlenging tot de oorspronkelijke lengte:

Hieruit volgt dat de rek een dimensieloze eenheid is. Een rek van 1 betekent dat de oorspronkelijke lengte verdubbeld is. Meestal is de relatieve verlenging echter subtieler van aard en wordt de rek uitgedrukt in promille of micron. Soms wordt ook de eenheid ‘S’ (strain) gebruikt om de hoeveelheid rek aan te geven.

De verhouding tussen de spanning en de rek wordt de elasticiteitsmodulus E van een materiaal genoemd, het geeft de weerstand tegen rek aangeeft. Stijve materialen hebben een hoge elasticiteitsmodulus en flexibele materialen een lage. Je kan je zo wel inbeelden dat rubber een zeer lage elasticiteitsmodulus heeft en glas heeft dan weer een hoge elasticiteitsmodulus. Hieronder zie je de de elasticiteitsmodulus (of Young-modulus) uitgezet voor bepaalde materiaalgroepen. In onderstaande grafiek wordt de elasticiteitsmodulus (Young’s Modulus) uitgezet ten opzichte van het soortelijk gewicht van de materialen, zo zie dat grosso modo zwaardere materialen eerder stijver zijn.

Young Modulus

We moeten dus vaststellen dat de wet van Hooke in feite meer een soort van vereenvoudiging is van het gedrag van materialen bij kleine rekken, maar dat de spanning-rek curve tot breuk per materiaal sterk kan verschillen. Glas zal zoals wel bekend plots breken, staal kan behoorlijk vervormen vooraleer er breuk is. Het gedrag van een materiaal na het elastisch gebied wordt het plastisch gebied genoemd. Het punt waarop een materiaal het elastisch gebied verlaat wordt het vloeipunt genoemd. Dat glas plots breekt heeft te maken met het ontbreken van een plastisch deel van de curve, een eigenschap van brosse materialen.

stress strain

En mocht je nu denken dat we vooral sterke en stijve materialen nodig hebben om veilige gebouwen te maken… dan heb je het helemaal mis! En dat heeft dan weer alles te maken met vervormingsenergie. Waarover later uiteraard meer…

Tot breuk uitgerekte groeten,

T.E.

In deze reeks:

Over structuren en de derde wet van Newton

Over structuren en het spannend verhaal van trekken en duwen

P.S.

Er wordt in de wandelgangen gefluisterd dat het, mede door het toedoen van de niet aflatende ijver van Newton om de herinnering aan Hooke zoveel mogelijk uit te wissen, geen portretten zijn overgebleven van de arme man. Het portret hieronder is een hedendaagse poging op basis van de overgeleverde geschreven info.

 

13_Portrait_of_Robert_Hooke

Geplaatst op door Tijs Essel · 1 reactie

Over structuren en het spannend verhaal van trekken en duwen

Er wordt niet enkel in wetenschappelijke kringen over spanning gesproken. Spanningen kunnen hoog oplopen tussen mensen of landen. Een boek kan spannend zijn. Ons dagelijks leven zit uiteraard ook vol stress (of spanning). We geven aan dat het een toestand is die in extremis kan leiden tot ruzie, oorlog, ontknoping of een zenuwinzinking… Een zwaar belastende job geeft je veel stress. De analogie voor materialen is zeer gelijklopend: een zwaar belast materiaal zal onder hoge spanning staan, totdat de spanning te hoog oploopt en het materiaal bezwijkt.

main-qimg-11a13227b43cff2cde6b30cc92816448

Als voorproefje voor dit schrijven had ik verkondigd dat krachten niet bestaan in realiteit (Over structuren en de derde wet van Newton), dat zal ik hier zeker niet ontkrachten, wel toelichten. Krachten bestaan niet in de zin dat een krachtvector een wiskundige constructie is zoals een rechte of een lijnstuk en daardoor geen breedte heeft en daarmee moeilijk verzoenbaar is met de werkelijkheid die zich in alle ruimtelijkheid voor ons ontplooit. In deze werkelijkheid is de spanning die optreedt in materialen een veel betere maatstaf van de toestand van een materiaal dan kracht. Bouwkundigen zullen daarom aan het einde van het verhaal vooral geïnteresseerd zijn in de spanningen die heersen in de materialen waarin constructies zijn opgebouwd, deze spanningen worden gedefinieerd als de kracht per oppervlakte:

stress_pic2

De Griekse kleine letter sigma wordt in de sterkteleer meestal als symbool gebruikt voor spanning en deze wordt uitgedrukt in Newton per vierkante meter (N/m²), algemene spanningen in de natuurkunde worden veelal uitgedrukt met het symbool p (pressure). De eenheid van spanning is pascal (Pa) waarbij 1 Pa = 1 N/ m². Deze eenheden maken deel uit van de uniforme internationale standaardeenheden (het SI-stelsel), en het pleit zeer voor de wereldwijde samenwerking van wetenschappers dat bijna alle landen diezelfde eenheden gebruiken. Het zou werkelijk onhandig zijn als bepaalde landen spanning in pakweg pond per vierkante duim zouden uitdrukken. Het is dan in het licht van de uniformisering betreurenswaardig dat we nota bene de Verenigde Staten van Amerika terug vinden in het rijtje van landen, naast Myanmar en Liberia, die niet officieel het SI-stelsel hebben ingevoerd. Dat maakt overigens dat bouwkundige naslagwerken (en ik vermoed bij uitbreiding veel wetenschappelijke boeken) uit de VS quasi waardeloos zijn in de rest van de wereld en de ontgoocheling is dan ook groot wanneer een aangekocht boek in deze middeleeuwse eenheden blijkt opgesteld te zijn. Voor degenen die toch de omrekening willen doen: 1 psi = ca. 6895 Pa, waarbij psi staat voor ‘pounds per square inch’.

psi kPa

Maar laten wij ons niet al te zeer verkneukelen in deze trans-Atlantische bizariteit. Wanneer wij spreken over een bloeddruk die 14 over 7 is dan spreken wij ook helemaal niet in pascal of N/m², maar hebben we het over kwikdruk in cmHg. Het was gebruikelijk om de luchtdruk te meten met behulp van een kolom kwik, de normale atmosferische luchtdruk bedraagt zo’n 760 mmHg. Kwik is veel zwaarder dan andere vloeistoffen, en daarom handiger qua formaat, zo is het historisch gegroeid dat mmHg de eenheid voor bloeddruk is geworden en 1 mmHg is trouwens gelijk aan ca. 133,322 Pa. De schaal is nu zo ingeburgerd dat het standaard is om lichaamsvloeistoffen uit te drukken in mmHg, voor alle andere toepassingen is het SI-stelsel de standaard. Een normale bloeddruk van 120 mmHg komt overeen met een druk van 16 kPa.

Het feit dat de luchtdruk op aarde schommelt rond 100 kPa (komt overeen met 1 bar) is op het eerste zicht verwonderlijk. Op ieder van ons heerst er een druk die equivalent is met een waterkolom van 10 m. Dat is een behoorlijke druk en zoals veel zaken die niet opvallen, valt hij pas op wanneer we hem moeten missen. Zoals op de maan, waar zonder ruimtepak onze lichaamssappen zouden koken, bij het ontbreken van voldoende luchtdruk, wat steeds tot een gewisse dood zou leiden. Dat doet me denken aan de koningin van de nacht uit De Toverfluit die zingt: “Der Hölle Rache kocht in Meinem Herzen”. Het bloed kookt in haar hart! Extreme drukken vinden we in het heelal: zowel het bijna absolute vacuüm in de verste leegtes van ons universum als de werkelijk extreme drukken binnen in een neutronenster. Daar heersen zo’n extreme drukken dat het onbegonnen is om ook maar enige vergelijking te maken. Toch een poging: een theelepeltje neutronenster weegt 10 miljoen ton, of evenveel als 50 keer het gewicht van de grootste containerschepen die er bestaan…

neutronenster

Maar terug naar spanningen in materialen, deze zijn nog een paar grootte ordes groter dan de luchtdruk en worden meestal uitgedrukt in MPa (één miljoen Pa). De maximale trekspanning in een materiaal wordt de treksterkte genoemd. Zo is de treksterkte van normaal staal 420 MPa. Hout is tien keer minder sterk: de sterkte van dennenhout is 40 MPa. Een enorm sterk materiaal is een koolstof nanobuis met een sterkte van maar liefst 62.000 MPa. En de treksterkte van beton sluit vele lijstjes van materialen af met een bedroevende 2 MPa.

Hoe is het mogelijk dat we zoveel gebouwen hebben opgetrokken met zo’n zwak materiaal als beton? Om dit te verklaren moeten we begrijpen dat spanningen zich manifesteren in twee verschijningsvormen: drukspanningen en trekspanningen. De luchtdruk is ontegensprekelijk een drukspanning, maar de treksterkte van materialen gaat over de trekspanningen. Beton heeft weliswaar een lage treksterkte, maar kan zeker z’n mannetje staan als het over druksterkte gaat. Dat is trouwens z’n sterkste punt, sterkteklassen van beton verwijzen altijd naar de druksterkte. Zo is C30/37 een beton met een karakteristieke druksterkte van 30 MPa op een proefcilinder (de 37 MPa slaat op de druksterkte op een proefkubus). Gewapend beton is een mooi huwelijk tussen beton en staal waarbij beton de drukspanningen voor z’n rekening neemt het staal de trekspanningen. Het gezegende aan dit huwelijk is dat beide materialen op dezelfde manier reageren op temperatuurschommelingen en dat beton het staal beschermd tegen corrosie.

Reinforced-Concrete

Dat spanningen een ander fenomeen zijn dan krachten kan je zelf ervaren als je een scherp potlood tussen duim en wijsvinger houdt en die samendrukt. De kracht in het potlood is uiteraard dezelfde, maar bij de kleine oppervlakte van de punt zal de spanning groter zijn (kracht gedeeld door kleiner oppervlak) en dat zie je ook afgetekend in je huid. Het is een welbekend voorbeeld dat een olifant gemakkelijker door het zand stapt dan iemand op stiletto’s. Dat heeft niets te maken met de kracht, maar alles met de spanning, want de spanning op de grond van de stiletto’s is veel groter dan de spanning veroorzaakt door een olifantenpoot. Laat ons dat eens snel berekenen voor een dame van 60 kg met hakken van diameter 1 cm diameter en een olifant van 5 ton met 4 poten met een diameter van 30 cm.

stiletto-elaphant

De druk onder een stiletto is wel 20 keer hoger dan de druk onder een olifantenpoot, daarmee loopt de olifant beduidend vlotter door het zand dan de dame in kwestie en begrijpt iedereen beduidend beter het verschil tussen krachten en spanningen.

Van de olifantenpoot naar een stevige kolom in een gebouw is maar een kleine stap het zijn allebei elementen waar er drukspanningen in heersen. Een mooi voorbeeld van trekspanningen zijn de spanningen in een kabel, en bij uitbreiding alle constructies die gebruik maken van kabels. Hangbruggen en tuibruggen zijn pareltjes van voorbeelden.

Cable-stayed-bridge-1000x500

Spanning. Het doet wat met een mens. Maar wat doet spanning met materialen? Vroeg of laat komt het tot breuk en sterke materialen zijn bestand tegen grote spanningen, maar hoe reageert een materiaal op spanning? We hadden het vorige keer over Newton en z’n wet over actie en reactie die aan de basis licht van de krachtenanalyse van een structuur. Maar minstens even belangrijk voor de bouwkundige analyse van structuren is de wet van z’n tijdsgenoot en rivaal: Robert Hooke. De wet van Hooke is werkelijk de Alfa en de Omega van de sterkteleer.

In een volgend schrijven zal de wet van Hooke onder de loep genomen worden, waarmee dit schrijven eindigt in spanning!

Spannende groeten,

T.E.

kisspng-hooke-s-law-shear-stress-strength-of-materia

Geplaatst op door Tijs Essel · 2 reacties

Over structuren en de derde wet van Newton

Newtons bewegingswetten toepassen op bouwkundige structuren lijkt op het eerste zicht een nutteloze onderneming. Structuren worden immers niet verondersteld te bewegen. Het liefst hebben we ze statig, solide en immobiel (vandaar ook immobiliën). Teveel beweging, laat staan een instorting, is uit den boze. Toch zijn structuren doordrongen van de derde wet van Newton. Die van actie en reactie! 

Structuren zijn er overal. Zoals iemand met een hamer overal nagels ziet en een leraar Nederlands overal taalfouten ziet, zo ziet een bouwkundige overal structuren. En dan zeker niet alleen in gebouwen. Ook een stoel, een kast, een ei, een boom, een huisjesslak, een verkeerslicht, een kartonnen doos, een glas en zelfs ons eigen lichaam zijn allemaal stuk voor stuk structuren. Het is niet voor niets dat ze soms spreken van een ‘kathedraal’ van een lichaam! En van simpel karton worden bouwkundigen werkelijk poëtisch: wat een prachtige mini-vakwerkjes komen immers te voorschijn wanneer je karton doormidden snijdt!

profipack_golfkarton_platen-7

De derde wet van Newton stelt dat wanneer een voorwerp A een kracht op een ander voorwerp B uitoefent, deze gepaard gaat met een even grote maar tegengesteld gerichte kracht van B op A. De woorden actie en reactie zijn wat misleidend want de krachten komen gelijktijdig voor, de ene is niet de oorzaak van de andere. De nagel slaat net zozeer op de hamer als de hamer op de nagel, met een even grote en tegengestelde kracht. Als een bokser z’n collega een welgemikte uppercut geeft, dan is het een magere troost voor laatstgenoemde dat de kracht van z’n kin terug op de bokshandschoen van z’n opponent precies even groot is. ‘Eat this!’, kan hij denken, net voor hij KO gaat, terwijl hij languit op de grond neergezijgd opnieuw een treffend voorbeeld is van de derde wet van Newton als interactie tussen z’n lichaam en de grond. Reciprociteit van krachten (of wederkerigheid) is een begrip die wellicht meer de lading dekt van de derde wet van Newton.

boksers met krachten

Ik weet niet welke job jij uitoefent, welke strijd er bij jou moet gestreden worden, maar bouwkundigen vechten tegen de zwaartekracht. Ze vechten tegen nog wel meer zaken, maar in hoofdzaak tegen de zwaartekracht, die vijand nummer één is van bouwkundige constructies. Het instorten van bruggen of gebouwen is een gebeurtenis waarbij de zwaartekracht wint. Het gebeurt gelukkig niet veel tijdens de levensduur waarvoor een constructie ontworpen is, maar als je maar lang genoeg wacht (op een geologische schaal), wint de zwaartekracht altijd.

Een muur is een eenvoudige constructie om de derde wet van Newton te illustreren. De muur oefent een kracht uit op de grond, en de grond oefent eenzelfde, tegengestelde  kracht uit op de muur. Hoe groter de muur, hoe groter de kracht, dat lijkt logisch. Want grotere muren zijn zwaarder, ze wegen meer. Die kracht is echter niet enkel de verdienste van de massa van de muur, maar evenzeer speelt de massa van de aarde hierin een rol. Eenzelfde muur op de maan, zal minder wegen.

muur 3de wet newton

Om de puntjes op de i te zetten zullen we hier nog eens de begrippen massa en gewicht door de mangel halen. Massa is onafhankelijk van het zwaartekrachtveld. Ook zwevend in de ruimte heb je een welbepaalde massa, maar aangezien er geen zwaartekracht is, heb je geen gewicht. De massa wordt uitgedrukt in kg, waar je ook heengaat blijft dit onveranderlijk. Het is echter de valversnelling die ervoor zorgt dat deze massa een welbepaalde kracht zal ondervinden die gelijk is aan de massa van het voorwerp vermenigvuldigt met de valversnelling: F=mg. Je zou vanaf nu heel logisch je gewicht in Newton (eenheid van kracht) kunnen uitdrukken, maar het is niet gegarandeerd dat hiervoor een sociaal draagvlak is…

Hoe kijkt een bouwkundige nu naar die muur? Een bouwkundige onderscheidt zich in alle bescheidenheid van de andere stervelingen op deze aardbol met het sublieme en tevens subtiele inzicht dat de interactie tussen de muur en de grond evengoed moet gelden voor de interactie tussen de rijen stenen van de muur. Steunen de bovenste 3 rijen immers niet op alle onderste stenen? Waar men ook een snede neemt geldt de derde wet van Newton! Het spreekt voor zich dat de snede-kracht in de onderste rij van de muur groter is dan de snede-kracht in de bovenste rij. En in feite is dat al een structurele analyse van de muur voor het belastinggeval van z’n eigen gewicht. Voor complexere structuren zoekt men ook de snedekrachten voor elke mogelijke snede van de structuur en de derde wet van Newton vertelt ons dat we in elke snede wederkerige krachten moeten vinden tussen deel A van de constructie aan de ene kant van de snede en deel B aan de andere kant van de snede.muur 3de wet newton

Kortom: we snijden in gedachten eender welke constructie doormidden en gaan op zoek naar de snedekrachten. Helaas is het niet zo simpel, want krachten bestaan in feite niet in de realiteit. Een straffe uitspraak, I know, maar het wordt helemaal duidelijk in het volgende deel ‘over structuren’.

Even grote en tegengestelde groeten,

T.E.

cartoon dikker en dikker 2

 

 

 

Geplaatst op door Tijs Essel · 1 reactie

Bladschikken voor gevorderden met de gulden snede

De gulden snede staat al eeuwen bekend als de perfecte esthetische verhouding. Er zijn heel wat gebouwen die volgens deze perfecte ratio gebouwd zijn. De Taj Mahal, het Parthenon, de Notre Dame in Parijs, overal zie je de gulden snede terugkomen. Maar wat wonderlijk is, is dat deze gulden snede ook in de natuur terugkomt. Bij veel planten en bloemen zijn de blaadjes geschikt volgens de gulden hoek, wat het equivalent is voor de gulden snede bij hoeken.

1-NGNon6GsqrUSrzMsF9vrEw

Mijn trans-Alpijnse zus heeft zonet een boek gelezen over de gulden snede: ‘La sezione aurea’. In het Italiaans klinkt dat zoveel mooier dan in het Nederlands, waar ‘gulden’ klinkt alsof het gaat om iets dat wat verguld is en kitsch, en snede is iets wat wij hier vooral associëren met een snee brood of het sneetje kaas dat we erop leggen. Een kitcherige boterham. Weg mystiek.

De gulden snede is de verhouding van twee lijnstukken waarbij het grootste zich verhoudt tot het kleinste, zoals de som van beiden zich verhouden tot het grootste lijnstuk.
Golden-Ratio-color-1024x439-1.png

Hieruit volgt de volgende uitdrukking:
Beide leden vermenigvuldigen met geeft de volgende kwadratische vergelijking:

met als positieve oplossing:

Een benaderende waarde voor de gulden snede is dus 1,618.

Mijn zus was vooral verwonderd over het verband tussen de gulden snede en de fyllotaxis. Dat heb ik toch eens moeten opzoeken, en dat blijkt de schikking van de blaadjes te zijn. Bladschikking blijkt voor planten van primordiaal belang te zijn. De fotosynthese is een proces waarbij licht moet opgevangen worden om koolstofdioxide (ook wel gekend als C02) om te zetten in koolhydraten. Een plant heeft er dus alle belang bij om z’n blaadjes zo te schikken dat ze zoveel mogelijk licht opvangen, en dat met een zo gemakkelijk mogelijke opdracht. In de DNA zou ergens kunnen de volgende opdracht weggeschreven zijn: schik het volgende blaadje onder een hoek  van het vorige blaadje.

Wat zou die hoek kunnen zijn? Als we =180° nemen, zien we al snel dat dit helemaal geen goede keuze is, want het derde blad komt boven het eerste blad te liggen. Ook 120° is geen goed idee, want na drie blaadjes ligt het vierde knal op het eerste blaadje, wat uiteraard niet efficiënt is voor de fotosynthese van de plant. We merken dat alle getallen die een gemakkelijke breuk vormen (360°/180°=2 en  360°/120°=3) geen goede oplossing zijn voor de bladschikking. Bij uitbreiding zijn alle rationele getallen vroeg of laat overlappend met vorige geschikte blaadjes. We zoeken dus een getal dat zich zo irrationeel mogelijk gedraagt.

Misschien is een goede keuze? Nee, want 22/7=3,142.. is al een zeer dichte benadering. Dat wil zeggen dat al veel te dicht aan het flirten is met de rationele getallen om bruikbaar te zijn voor een nuttige bladschikking. Dit kan men goed zien als we de enkelvoudige kettingbreuk van uitzetten:
Als we de kettingbreuk afbreken bij 7 dan krijgen we de verhouding 22/7. Hele grote getallen zorgen in een kettingbreuk voor een goede benadering met rationele getallen. Zo is 355/113=3.14159292… een zeer goede benadering voor . Dit komt omdat het volgende getal in de kettingbreuk een heel groot getal is: 292.

Als grote getallen in een kettingbreuk leiden tot getallen die zich gemakkelijk laten benaderen door een rationeel getal, kunnen we dus ook omgekeerd zeggen dat een kettingbreuk met kleine getallen zal leiden tot een zeer irrationeel getal. En het meest irrationele getal dat we kunnen bekomen is een kettingbreuk met alleen maar eentjes:

Het zal je niet verwonderen dat deze uitdrukking in deze tekst die handelt over de gulden snede effectief perfect gelijk is aan de gulden snede:

Terug naar de plant met de DNA opdracht: schik de blaadjes volgens de gulden hoek. De gulden hoek wordt uitgedrukt als:

Dat is de kleinste hoek van twee hoeken die een volledige cirkel verdelen in twee hoeken volgens de gulden snede: 137,5°+ 222,5°=360° en 222,5/137.5=1,1618…

Hieronder zie je de eerste 5 blaadjes van een plant geschikt volgens de gulden snede, de blaadjes bevinden zich telkens een hoek 137,5° verder van elkaar. Of 222,5° in tegenwijzerzin.

Leaf-Growth-5.png

Zo gaat het door en door en we verkrijgen telkens een zo minimale overlap met de vorige blaadjes.

Leaf-Growth-13.png

Ook bij de schikking van de zaadjes in een zonnebloem gebeurt iets gelijkaardig. De zaadjes zijn allemaal geschikt volgens de gulden hoek. Dit levert immers de meeste zaadjes op een zo klein mogelijke oppervlak op. Hieronder kan je zien dat een kleine variatie van de hoek al een veel minder gunstige schikking oplevert van de zaadjes.Sunflower-seed-golden-angle-diagram.001.pnglabimg_870_Sunflower

Als je je nu de bedenking maakt: amai hoe kan dat? Dan moet je maar denken aan het feit dat alle minder gunstige variaties in de natuur met minder gunstige hoeken het niet hebben overleefd ten opzichte van de planten met een gunstigere schikking. Wat we in de natuur vinden is het product van een proces van miljoenen jaren variatie, overerving en selectie. (lees ook: Hoe intelligent is de hemelse horlogemaker?) Je zou het sommige mensen niet aangeven, maar ook die zijn het product van miljoenen jaren van finetuning.

Oh ja en dan hebben we ook nog de wonderbaarlijke Fibonacci getallen: 1,1,2,3,5,8,13,… waarvoor geldt dat het volgende getal telkens de som is van de twee vorige getallen. Er zijn in de natuur ook veel Fibonacci getallen te vinden… Mysterieus van de natuur? Helemaal niet want laten we eens de gulden snede benaderen door de kettingbreuk af te breken dan krijgen we volgende benaderingen:

Twee opeenvolgende Fibonacci getallen blijken dus een steeds betere benadering van de gulden snede te zijn naarmate we verder gaan in de Fibonacci rij:

De natuur vond immers ook dat, als we dan toch getallen of een verhouding gebruiken in het bladschikken of het zaadschikken,  we maar beter Fibonacci getallen kunnen gebruiken.

Je hoeft trouwens niet  met de eerste Fibonacci getallen 1 en 1 te starten om uit te komen op de gulden snede. Neem eender welke twee getallen en tel ze samen en maak dan telkens de som van de laatste twee getallen en je komt sowieso altijd uit op de gulden snede. Als je pakweg 37 en 11 neemt zal dit ook een reeks vormen waarvan de verhoudingen op de limiet de gulden snede zijn. Ik heb het niet nagegaan, maar het moet wel gewoon altijd lukken. Dat is niet echt een straf wiskundig bewijs, maar dat laat ik over aan anderen.

Nu ik erover nadenk. Net omdat de gulden snede het meest irrationele getal is dat we kunnen bedenken zal het waarschijnlijk totaal geen streling voor het oor zijn als we twee klanken zouden laten samenklinken waarvan de verhouding van de frequenties gelijk is aan de gulden snede. Want enkel eenvoudige verhoudingen van gehele getallen zijn harmonische tweeklanken. (zie ook: Alle piano’s zijn een beetje vals). Dat is toch wat anders dan je zou verwachten van deze sectio divina, of goddelijke verhouding.

We kunnen besluiten dat de gulden snede hoogstwaarschijnlijk leidt tot het meest irritante, dissonante en valse interval in de hele muziekwereld. Geen idee of dat ook in het boek van mijn zus stond. Ik hoor het wel binnenkort!

Zorgvuldig in het lente-zonlicht geschikte groeten,

T.E.

Geplaatst op door Tijs Essel · 2 reacties

Wat kleuters en hooligans al lang weten over de gevolgen van aardbevingen…

We willen uiteraard niet dat het gebouw, waar we ons in vertoeven, als een kaartenhuisje in elkaar stuikt wanneer de aarde aan het schudden gaat, een gebeurtenis die in onze contreien gelukkig eerder zeldzaam is. De wetenschap nodig om gebouwen sterk genoeg te maken is onder andere gebaseerd op de eigenfrequentie van de structuur, en dat is iets waar kleuters en hooligans veel meer over weten dan we denken…

registratie

Een aardbeving is een goed gekozen woord, want een aardbeving is samengesteld uit vele trillingen met een frequentie en een amplitude. Het spreekt vanzelf dat de amplitude een graad is voor de zwaarte van een aardbeving, maar ook de frequentie speelt een grote rol in de manier waarop een gebouw zal reageren. Ondertussen zijn er tal van aardbevingen geregistreerd en weet men welke amplitudes en frequenties kunnen optreden bij aardbevingen, en met gesofisticeerde software kun je zelfs een gebouw virtueel blootstellen aan een reeds opgetreden aardbeving, waarvan de parameters gekend zijn.

We moeten dus een analyse maken van de manier waarop een structuur zal reageren bij dynamische belastingen. Dat is gemakkelijker gezegd dan gedaan, daarom gaan we eens kijken waar we trillingen waarnemen rondom ons. Op dit moment hoor ik bijvoorbeeld de wasmachine vertragen van toerental en als je er goed op let lijken de bewegingen bij een bepaalde lage frequentie veel heviger dan bij een hoger toerental. We stellen dus vast dat een wasmachine een eigenschap heeft, waarbij hij lijkt te willen dansen bij een bepaalde frequentie. Deze frequentie noemen we de eigenfrequentie.

Maar dat moet je niet aan kleuters uitleggen, want die rennen naar een schommel en vinden zonder enig probleem de eigenfrequentie van het systeem. Ook hooligans moet je niet lastigvallen over wiskundige formules betreffende het dynamisch gedrag van een stilstaande interventiewagen. Ze vinden feilloos de eigenfrequentie van het voertuig en weten precies wanneer ze een extra duwtje moeten geven om het ongelukkige voertuig te kapseizen. En dat doen ze trouwens altijd volgens de dwarse en dus zwakke richting van het systeem, zonder dat ze de kwadratische oppervlaktemomenten hebben berekend. Straf toch.

Zoals een wasmachine, een schommel en een voertuig hebben gebouwen ook frequenties waarbij ze gemakkelijker trillen, deze frequenties zijn afhankelijk van de eigenschappen van het gebouw (gebruikte materialen, stijfheid, vorm, hoogte,..). Je kan je wel inbeelden dat voor een hoog regelmatig gebouw het heen en weer bewegen een basisvervorming zal zijn, die hoort bij een bepaalde frequentie. Als de aardbeving net trilt op die basisfrequentie (horende bij de basisvervorming), dan zullen de krachten op het gebouw zeer groot worden (denk maar aan de hooligans die altijd net op het juiste moment een duwtje geven tegen een voertuig) en die zullen aanleiding geven tot grote vervormingen. Dit alles kan leiden tot het bezwijken van het gebouw, zeker wanneer de amplitude (het aantal hooligans in onze analogie) groot is. Je zou kunnen zeggen dat er resonantie is van het gebouw met het trillen van de aarde.

Niet alleen het trillen van de aarde kan resonantie veroorzaken in een constructie. Er bestaat een filmpje van de Tacoma Narrow Bridge waarbij de resonantie werd veroorzaakt door de wind, maar met niet minder fatale gevolgen voor de constructie van de hangbrug. Los van de resonantie een ‘cool’ filmpje om te zien. Maar het bezwijken had dus niets met aardbevingen te maken. En dat is net zo tof aan wetenschap dat je alles wel ergens aan elkaar kunt linken, maar toch niet helemaal.

Wat zorgt er nu voor dat een gebouw tegen een duwtje kan? Vooreerst moet het gebouw goed gefundeerd zijn. Als de grond verzakt tijdens een seismische gebeurtenis, dan zal het gebouw uiteraard mee bewegen. Hoewel het meestal een goed plan is om een gebouw zo stijf en zo sterk mogelijk te ontwerpen, is er toch een iets andere denkwijze nodig in het ontwerp tegen aardbevingen, en dat heeft alles te maken met het dissipatievermogen van het gebouw. Dissi-wat?

De dissipatie is de absorptie van de energie (van de aardbeving) door het plastisch gedrag van het gebouw. In feite is het opnieuw logisch te begrijpen als we het vergelijken met een auto die botst tegen een muur. Als je in die auto zit dan zal je blij zijn dat de auto-ontwerper een kreukelzone heeft voorzien tussen jezelf en de voorkant van de auto (even in de veronderstelling dat je frontaal tegen die muur bent gereden). Die kreukelzone absorbeert de energie van de botsing. En dat willen we ook zoveel mogelijk introduceren in een gebouw.

Hoe meer kreukelzones in het gebouw, hoe groter het dissipatieve vermogen van het gebouw, hoe meer we op ons twee oren kunnen slapen bij een aardschok. En omdat niemand hen zou begrijpen hebben wetenschappers ook hier afkortingen geïntroduceerd… wanneer ze spreken van DCL, DCM of DCH, bedoelen ze dus respectievelijk ‘ductility class low’ (geen kreukelzones), ‘ductility class medium’ (kreukelzones) en je raadt het al DCH is ‘ductility class high’, wat staat voor een gebouw met een zeer groot dissipatief vermogen. Het verfrommelt serieus maar het kan wel tegen een duw zonder in te storten.

Iedereen doet er eigenlijk goed aan om bij een botsing zoveel mogelijk zich te gedragen als een kreukelzone. Zo stappen ladderzatte passagiers, die zich gedragen als een zak patatten, soms zonder kleerscheuren uit een auto, terwijl de meer nuchtere reisgezellen, die zich schrap hebben gezet (verhoogde stijfheid), meerdere breuken oplopen.

Mijn welgemeende excuses mocht ik hiermee mensen op bizarre ideeën hebben gebracht, maar het is gewoon toegepaste wetenschap!

Dissipatieve groeten,

T.E.

Geplaatst op door Tijs Essel

Hoe sterk is een biljet van 10 euro?

Hoe harder je trekt hoe langer het wordt … en hoe harder je duwt hoe korter het wordt. Dit lijkt niet meteen de meest spectaculaire wetenschappelijke vondst en het lijkt ook niet meteen iets wonderlijk of ingewikkeld, maar het is toch het grondbeginsel waar een bouwkundig ingenieur dag in dag uit mee aan de slag gaat. 

In het latijn klinkt het natuurlijk iets ‘spannender’ : ‘Ut tensio sic vis’. Zo de rek, zo de kracht. Ook wel gekend als de wet van Hooke. Maar het is eigenlijk niet echt een wet, zoals de wetten van Newton, maar meer een materiaalvergelijking die slechts beperkt opgaat. Want als je te hard trekt, dan weet iedereen dat het vroeg of laat breekt. Het ene materiaal al sneller dan het andere, maar zelfs de beste rekker begeeft het op een gegeven moment.

Het is een wetmatigheid dat voor quasi alle materialen opgaat. De mate waarin iets verlengt zal uiteraard afhankelijk zijn van het materiaal, zo is het duidelijk dat een rekker gemakkelijker zal uitrekken dan een stalen lat. Maar dat het materiaal zal verlengen staat buiten kijf. Dat gaat ook op voor je eigen lichaam, dat belast je ook door rechtop te lopen. Daarom ben je ’s morgens ook altijd langer dan ’s avonds. ’s Avonds ben je moe, versleten en dus ook een beetje korter…

De stijfheid van een bepaalde constructie is de moeilijkheid om het te verlengen of meer algemeen te vervormen. De stijfheid is afhankelijk van het gebruikte materiaal en ook afhankelijk van de vorm. Hier dringt zich uiteraard een klein voorbeeldje op. Stel dat je wil bungee-jumpen. Dan zijn er twee dingen waar je je zorgen over maakt: zal de schok niet te groot zijn en zal de rekker het houden. Een lage stijfheid zal ervoor zorgen dat er voldoende vervorming mogelijk is: dus het materiaal elastiek is goed gekozen. Maar of de rekker het zal houden is ook afhankelijk van de dikte van de rekker: geen zinnig mens wil van de brug springen aan een elastiekje waarmee je je brooddoos dichthoudt.

Over zinnige mensen gesproken… Er is een verhaal van een bepaald persoon die geen rekening gehouden had met de wet van Hooke. Hij wou een bungee-sprong doen van een 20 m hoge brug en deed netjes z’n huiswerk en zocht een bungee-rekker die een paar meter korter was dan 20 m zodat hij met een gerust gemoed… te pletter viel, want hij had geen rekening gehouden met de verlenging van het koord. Het leverde hem in 1999 de Darwin Award op, een cynische eer die wordt gegeven aan mensen die “bijdragen” aan de menselijke evolutie door zichzelf op een domme manier te laten verongelukken waardoor hun genen verwijderd worden uit de genenpoel der mensheid.

Even terug naar de bouwkunde, waar alles min of meer draait rond deze materiaalvergelijking. Het lijkt een simpel gegeven, je zou je zelfs afvragen waarom er zoveel jaar nodig is om een bouwkundig ingenieur te worden als het enige dat je moet weten is dat iets meer verlengt als je er harder aan trekt. Dat komt omdat dat verlengen en verkorten in een constructie overal anders is. Zelfs bij een eenvoudige constructie zoals een plank over een grachtje heb je bovenaan materiaal dat verkort en onderaan materiaal dat verlengt, zodat de plank gaat buigen. Dus je kan trekken en duwen tezamen hebben in een doorsnede. Omdat dat zoveel voorkomt hebben bouwkundigen het trekken en duwen ‘buigend moment’ genoemd.

De weerstand van een constructie om te buigen is de buigstijfheid, en die kom je in veel formules die de doorbuiging berekenen tegen als ‘EI’, waarbij E staat voor de stijfheid van het materiaal en I voor de vorm van de doorsnede. Zonder verder dieper in te gaan op onderstaande tabel, moet je je ogen maar eens laten glijden over alle EI-buigstijfheden die in de formules staan…beam-formulas-2-638

Het is dus de opdracht van een bouwkundig ingenieur om een constructie ‘slim te ontwerpen’ om de wet van Hooke te slim af te zijn. We willen een constructie ontwerpen waarin de spanningen, en dus vervormingen zo klein mogelijk blijven. Als een lat niet mag buigen, is het evident dat je de lat niet plat houdt, maar recht. Dat wil zeggen dat we sterkere constructies kunnen maken door balken recht te zetten en niet plat…

Om af te sluiten heb ik een klein experimentje opgezet om een biljet van 10 euro sterker te maken door een slim ontwerp. Wanneer we een biljet opleggen tussen twee bierpotten blijkt dat het gewicht van een stuk van 2 euro al veel te zwaar is en dat de ‘constructie’ bezwijkt.

Nu is het de bedoeling om door te spelen met de vorm van de doorsnede de constructie zo sterk mogelijk te maken. Ik heb ervoor gekozen om het biljet te op te vouwen als een accordeon om zo de stijfheid te verhogen, zo probeer ik om het platte briefje zoveel mogelijk te laten werken als balkjes …

Zou de nieuwe constructie nu het 2 euro stuk wel kunnen dragen?

 

 

 

 

 

 

 

 

Of zou het zelfs nog iets zwaarder kunnen dragen?

 

 

 

 

 

 

 

Wie zal het zeggen?

 

 

 

 

 

 

Het is uiteindelijk maar papier hé…

 

 

 

 

 

 

Maar wel geplooid door een bouwkundig ingenieur…

 

 

 

 

 

 

Tja… wat kent die van plooien?

 

 

 

 

 

 

Hier komt het:

 

 

 

 

 

 

 

 

 

 

 

 

 

Tadaa!

We kunnen een volledige volle bierpot dragen met het briefje van 10 euro! Dat wil zeggen dat we met een slim ontwerp dus wel degelijk het verschil kunnen maken…

Dus toch iets geleerd tijdens mijn jaren opleiding bouwkundig ingenieur… en nu vlug opdrinken vooraleer de constructie bezwijkt… ook dat heb ik gelukkig geleerd tijdens mijn jaren opleiding!

Bouwkundige groeten,

T.E.

 

20181124_191049