Wanneer ik mijn dochters kamer betreed, word ik geconfronteerd met één van de meest fundamentele natuurwetten. Het is een wetmatigheid die nog fundamenteler is dan dan de wetten van Maxwell of de relativiteitsleer. Het is het onomkeerbare proces van nuttige energie naar nutteloze energie, dat in één adem ook nog eens de richting van tijd vastlegt. Het is inderdaad de wet van de stijgende entropie waar ik aan herinnerd word terwijl ik me een weg baan doorheen speelgoed, kleren en knuffels in mijn dochters kamer.

Het niet zo tot de verbeelding sprekende maar toch algemeen bekende entropie-experiment is het plaatsen van een bord warme soep in een kamer en dan kijken wat er gebeurd. De soep zal afkoelen en de kamer zal heel lichtjes opwarmen door de warme soep, maar de feitelijke vraag is waarom dit gebeurt. De analogie met mijn dochters kamer is ook snel gemaakt: we laten haar een paar uur spelen in de kamer en dan checken we de toestand. Ook hier zal de vaststelling zijn dat de kamer geëvolueerd is naar een toestand waarin het speelgoed overal rond ligt, eerder dan dat we zouden verwachten dat die netjes opgeruimd blijft. In beide gevallen evolueert het systeem naar een evenwichtssituatie, waarbij de entropie maximaal wordt. Bij de soep gaat het over de verspreiding van de energie bij een bepaalde temperatuur, daarom is de eenheid van entropie energie (Joule) per temperatuur (Kelvin): J/K.

Om een meer exacte verklaring te geven over het waarom van bovenstaande processen moeten we spreken over de waarschijnlijkheid van toestanden. Het lijkt misschien bizar om bij het soepbord-experiment te gaan spreken over waarschijnlijkheden, want je bent in feite zeker dat het nieuwe evenwicht zal ontstaan. Om duidelijk te maken dat entropie alles te maken heeft met de waarschijnlijkheid van toestanden, kunnen we bij de kamer van mijn dochter eens gaan kijken naar de waarschijnlijkheid. We vereenvoudigen sterk de kamer en veronderstellen dat er slechts 2 posities zijn waarin speelgoed of andere kameringrediënten zich kunnen bevinden en dat we de positie waarin alles in één positie ligt, kunnen beschouwen als een opgeruimde kamer. Laten we eerst even een kamer nemen met 2 posities en 2 spullen, haar pop Meesje en een rondslingerende schoen.

We stellen vast dat er 4 mogelijke toestanden zijn, 2 toestanden zijn opgeruimde toestanden en er zijn 2 rommel-toestanden. Dat betekent dat de waarschijnlijkheid dat in dit sterk vereenvoudigd systeem de kamer er opgeruimd zal uitziet 50% is. Doordat er amper 2 spullen en 2 posities zijn, is er in dit geval nog een goede kans dat we na een tijdje toch terugkeren naar een opgeruimde toestand. Maar als we het aantal spullen verhogen dan bemerken we een verandering van de kans op ‘opgeruimde toestand’. Laten we ter illustratie het aantal spullen even verdubbelen naar 4: we vullen de pop en de schoen aan met een knuffel en een auto, en beschouwen nu de kans op ‘opgeruimde kamer’.

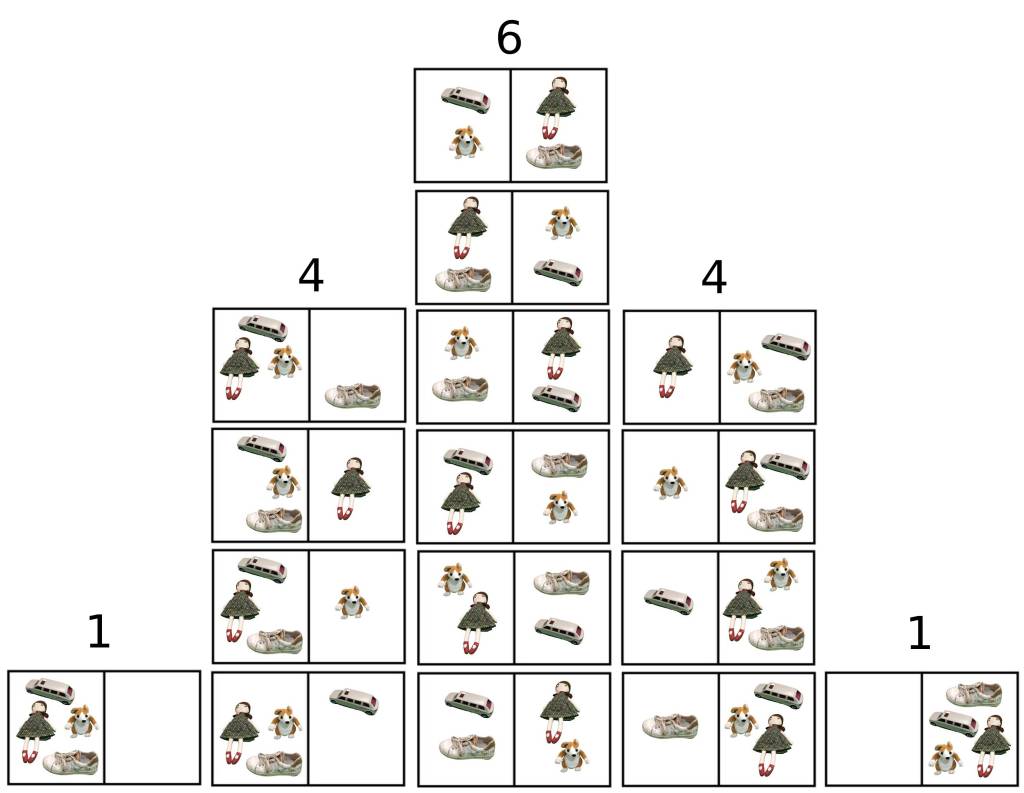
We kunnen vaststellen dat het aantal mogelijke toestanden toegenomen is tot 16. Om de correcte terminologie te gebruiken spreken we per individueel geval van een microtoestand en per globale toestand (bv. 1 spul ligt links 3 spullen rechts) spreken we van een macrotoestand. Bij macrotoestanden verliezen we de info over individuele toestanden, en deze link naar informatie maak ik niet zomaar, want ook in de informatietheorie is entropie een belangrijke grootheid. De eenheid van entropie in deze tak van de wetenschap is bit en de entropie van de informatie is gelijk aan het gemiddeld aantal ja-of-nee-vragen die gesteld moeten worden om de informatie te achterhalen. Als de info die je wenst mee te geven één van je ouders is, dan is dit te achterhalen met één ja-of-nee-vraag, dus is de entropie van die informatie één bit. Als de info een bepaalde letter is van het alfabet, ergens in een tekst, dan zal de kans op voorkomen van elke letter bepalend zijn om de entropie te bepalen van de informatie die besloten ligt in die letter.

Terug naar de kamer met spullen. Het is gemakkelijk in te zien dat bij het verder toenemen van spullen de mogelijkheden exponentieel zullen toenemen. Bij 2 mogelijke posities in de kamer en n spullen zal het aantal mogelijke toestanden 2ⁿ zijn. Bij 10 spullen zijn die mogelijke toestanden 1024, dus dat loopt wel snel op. (zie ook: Schaakmat voor koning Shirham). Het gevolg is dat de kans op ‘opgeruimde toestand’ dramatisch daalt bij toenemende spullen in de kamer. Zo is de kans op een opgeruimde kamer bij 4 spullen nog maar 12,5% (14 van de 16 toestanden zijn rommel-toestanden) en bij 10 spullen nog maar amper 0,2%.

Zonder dat we goed beseffen zijn we terecht gekomen in een binomiaal-verdeling, ook wel bekend van de kop-of-munt experimenten (dit eenvoudige toevalsexperiment wordt een Bernoulli-experiment genoemd). Het plaatsen van een bepaalde hoeveelheid spullen in één van de twee posities komt overeen met het uitvoeren van een zelfde aantal kop-of-munt experimenten. En wanneer we het aantal spullen nog laten toenemen gebeurt er iets heel curieus, en ook iets heel logisch. De oppervlakte onder elke grafiek is gelijk genomen aan 1, zodat we direct kansen kunnen aflezen en de discrete grafiek is continue gemaakt.

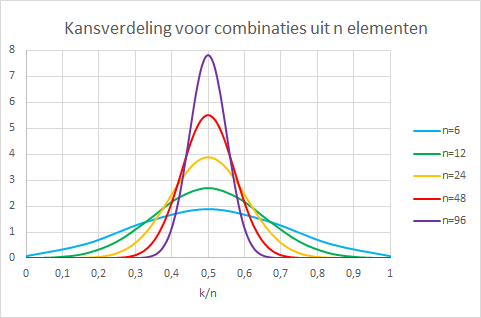
Het curieuze is dat de grafiek evolueert naar een normaalverdeling (de welbekende klokvorm), dat volgt uit de centrale limietstelling die stelt dat voor (bijna) gelijk welke soort kansverdeling (bv 50% kop of 50% munt) de verdeling van de gemiddeldes uit verschillende experimenten normaal verdeeld zijn. Als je er even over nadenkt is dat wel heel curieus, maar we zien het in de grafiek voor onze ogen gebeuren. En het logische is dat de grafiek smaller en smaller wordt, tot alle waarden zich in een minieme band rond het gemiddelde zullen bevinden. Dat betekent dat er altijd maar minder kans is op variatie van het gemiddelde. Als je heel lang kop-of-munt gooit zal je uiteindelijk met zeer hoge nauwkeurigheid in de buurt van 50% komen. Deze zeer hoge nauwkeurigheid is wat we vaststellen als we de temperatuur van iets gaan meten. Temperatuur is de hevigheid van het trillen van deeltjes. Het is bijlange niet zo dat alle deeltjes met precies dezelfde hevigheid trillen, maar we kunnen wel met zekerheid zeggen dat de gemiddelde trilling, dus de temperatuur niet fluctueert. De wet van de grote getallen zorgt ervoor dat de temperatuur gewoon een vaste waarde is.

Nu is het moment er gekomen om de meest beroemde formule van de (statistische) entropie tentoon te spreiden: S=k ln W, beter bekend als de formule van Boltzmann. Waarbij S staat voor de entropie, en W voor het aantal manier waarop een toestand mogelijk is. Bij systemen met miljoenen, miljarden deeltjes zal er niet meer gesproken worden over een kansverdeling, maar over het aantal mogelijke posities. De factor k is er enkel om de energieboekhouding goed te krijgen tussen eenheden, zodat entropie in J/k kan uitgedrukt worden. De formule van Boltzmann is in feite ook een soort gemiddelde en geldig bij grote aantallen microtoestanden (bv bij een gas). De statistische wet van de grote aantallen zorgt ervoor dat dat de de formule van Boltzmann geldig is bij grote aantallen, zoals toestanden van gassen in de natuurkunde. Als we heel veel spullen laten rondslingeren in de twee mogelijke posities, zal precies de helft in de eerste positie zitten en precies de andere helft in de tweede positie zitten. Dit is hetzelfde evenwicht dat we ervaren bij de druk in een ballon, of de temperatuur van een systeem in evenwicht.

Er kan ook redelijk eenvoudig aangetoond worden waarom de logaritme nodig is in de formule. De entropie van een systeem is immers een extensieve grootheid, dat wil zeggen dat de entropie evenredig moet zijn met het aantal deeltjes. Dus als we tien keer zoveel deeltjes nemen, willen we ook dat de entropie maal tien gaat. Wiskundig gezien is er een manier om de exponentieel stijgende toestanden toch evenredig te krijgen met het aantal deeltjes en dat is door de logaritme te nemen van de de mogelijke toestanden. Zo blijft de entropie netjes evenredig met het aantal deeltjes, terwijl de mogelijke toestanden exponentieel stijgen.

Entropie heeft dus alles te maken met waarschijnlijkheid. Het stijgen van de totale entropie is equivalent met wat het meest waarschijnlijke zal gebeuren. Daarom is entropie ook zo sterk gelinkt met de richting van de tijd. Als je een glas laat vallen is het meest waarschijnlijke dat één van de miljoenen, miljarden toestanden waarop een glas gebroken kan zijn zal ontstaan, en is het onnoemelijk onwaarschijnlijk dat die ene toestand waarbij het glas intact blijft wordt bereikt. Net omdat er zoveel mogelijkheden zijn op een gebroken glas kunnen we met complete zekerheid voorspellen dat het glas zal breken.

Omdat waarschijnlijk het waarschijnlijke zal gebeuren stijgt de entropie, en dat is in feite een veel exactere (en volgens mij meer duidelijke) omschrijving dan ‘chaos die toeneemt’ of ‘wanorde die stijgt’. Daarom sta ik dus met aan zekerheid grenzende waarschijnlijkheid te waden in de rommel van mijn dochters kamer. Eerst wou ik afsluiten met: ‘het is niet het einde van de wereld, die stijgende entropie’, om de boel wat te relativeren. Maar daar moet ik helaas op terugkomen. Het is de mogelijke drijfveer voor het einde van het heelal want nadat alle materie zich verliest in zwarte gaten (grootste entropietoestand voor gravitatie) zullen deze verdampen door hawkingstraling en eindigt het heelal in een warmtedood, het finale thermodynamische evenwicht… en graag eindig ik met deze vrolijke noot.

Veel entropisch gemaximaliseerde groeten,

T.E.